题目内容
我们的银河系的恒星中大约四分之一是双星。某双星由质量不等的星体A和B构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动。由天文观察测得其运动周期为T,A和B的距离为r,已知引力常量为G。由此可求出两星的质量之和为 。
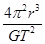
解析试题分析:设两颗恒星的质量分别为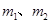 ,做圆周运动的半径分别为
,做圆周运动的半径分别为 ,角速度分别为
,角速度分别为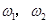 .根据题意有
.根据题意有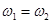 ①
① 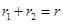 ②
②
根据万有引力定律和牛顿定律,有
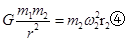 联立以上各式解得
联立以上各式解得 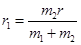 ⑤
⑤
根据解速度与周期的关系知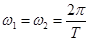 ⑥
⑥
联立③⑤⑥式解得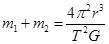 ⑦
⑦
考点:万有引力定律及其应用.
点评:本题是双星问题,与卫星绕地球运动模型不同,两颗星都绕同一圆心做匀速圆周运动,关键抓住条件:相同的角速度和周期.

练习册系列答案
相关题目
我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.那么S1、S2做匀速圆周运动的( )
| A、角速度与其质量成反比 | B、线速度与其质量成反比 | C、向心力与其质量成反比 | D、半径与其质量的平方成反比 |