题目内容
11. 如图所示,在磁感应强度为B,方向竖直向下的匀强磁场中,相距为L的两根足够长平行光滑金属轨道MN、PQ固定在水平面内,一质量为m、电阻为R1的导体棒ab垂直轨道旋转且与轨道电接触良好,轨道左端M点接一单刀双掷开关S,P点与电动势为E,内阻为r的电源和定值R2相连接,不计连轨道的电阻.
如图所示,在磁感应强度为B,方向竖直向下的匀强磁场中,相距为L的两根足够长平行光滑金属轨道MN、PQ固定在水平面内,一质量为m、电阻为R1的导体棒ab垂直轨道旋转且与轨道电接触良好,轨道左端M点接一单刀双掷开关S,P点与电动势为E,内阻为r的电源和定值R2相连接,不计连轨道的电阻.(1)求开关S合向1瞬间导体棒的加速度a;
(2)开关S合向1,在导体棒速度等于v时把S合到2,导体椴又向右运动距离x后停下,求S合到2的瞬间导体棒ab两端的电压U及此后通过导体棒的电荷量q1;
(3)若从开关S合向1到导体棒速度等于v的过程中,通过电源的电荷量为q2,求此过程中导体棒ab上产生的焦耳热Q1.
分析 (1)由闭合电路欧姆定律求出电路中的电流,再由安培力公式F=BIL求得力的大小,再由牛顿第二定律得到加速度a;
(2)S合到2的瞬间导体棒ab切割磁感线,由E=BLv求出感应电动势,由串联电路分压规律得到ab两端的电压U.
根据法拉第定律、欧姆定律和电量公式q=It结合求得通过导体棒的电荷量q1;
(3)根据能量守恒定律和串并联电路特点求解ab上产生的焦耳热Q1.
解答 解:(1)开关S与1闭合瞬间,由闭合电路欧姆定律得:
此时通过导体棒的电流 I=$\frac{E}{{R}_{1}+r}$
由安培力:F=BIL
由牛顿第二定律有 F=ma
解得 a=$\frac{BLE}{m({R}_{1}+r)}$
(2)导体棒速度等于v时产生的感应电动势 E1=BLv
ab两端的电压 U=$\frac{{R}_{2}{E}_{1}}{{R}_{1}+{R}_{2}}$
解得 U=$\frac{BLv{R}_{2}}{{R}_{1}+{R}_{2}}$
此后过程中产生的平均感应电动势 $\overline{E}$=$\frac{△Φ}{△t}$
通过导体棒的电荷量 q1=$\overline{I}△t$=$\frac{\overline{E}}{{R}_{1}+{R}_{2}}$•△t
而△Φ=BLx
可得 q1=$\frac{BLx}{{R}_{1}+{R}_{2}}$
(2)设此过程中电路中产生的焦耳热为Q,则 q2E=Q+$\frac{1}{2}m{v}^{2}$
导体棒ab上产生的焦耳热 Q1=$\frac{{R}_{1}}{{R}_{1}+r}$Q
解得 Q1=$\frac{{R}_{1}}{2({R}_{1}+r)}$(2q2E-mv2)
答:
(1)开关S合向1瞬间导体棒的加速度a为$\frac{BLE}{m({R}_{1}+r)}$;
(2)S合到2的瞬间导体棒ab两端的电压U为$\frac{BLv{R}_{2}}{{R}_{1}+{R}_{2}}$,此后通过导体棒的电荷量q1为$\frac{BLx}{{R}_{1}+{R}_{2}}$.
(3)此过程中导体棒ab上产生的焦耳热Q1为$\frac{{R}_{1}}{2({R}_{1}+r)}$(2q2E-mv2).
点评 本题从力和能量两个角度分析电磁感应现象,根据法拉第定律、欧姆定律推导出安培力F=$\frac{{B}^{2}{L}^{2}v}{R+r}$,这是常用的经验公式,要能熟练推导.对于导体棒切割类型,关键要正确分析受力,把握其运动情况和能量转化关系.

| A. | 光能在弯曲的光导纤维中传播,说明光在同种均质介质中是沿曲线传播的 | |
| B. | 白光照射到DVD片表面时出现彩色是因为光具有波动性 | |
| C. | 某参考系中的两处同时发光,在另一惯性参考系中观察一定也是同时发光 | |
| D. | 真空中的光速在不同惯性参考系中相同,因此光的频率与参考系无关 |
| A. | 肥皂膜在阳光的照射下呈现彩色是光的干涉现象造成的 | |
| B. | 根据麦克斯韦电磁理论,变化的磁场一定能产生变化的电场 | |
| C. | X射线在电场中能够发生偏转 | |
| D. | 波的频率与振源的频率相同 |
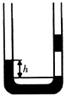 如图所示,两端开口的U型管中装有水银,在右管中用水银封闭着一段空气,要使两侧水银面高度差h增大,应( )
如图所示,两端开口的U型管中装有水银,在右管中用水银封闭着一段空气,要使两侧水银面高度差h增大,应( )| A. | 从左管滴入水银 | B. | 从右管滴入水银 | C. | 让气体升温 | D. | 增大大气压强 |
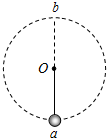 如图所示,长度为L的轻质细杆的一端与质量为m的小球相连,可绕过O点的水平轴自由转动.现在最低点给小球一水平初速度v0,使它能在竖直平面内做圆周运动.设小球在轨道最低点a和最高点b受到细杆的作用力大小分别为F1和F2,重力加速度为g,则下列判断正确的是( )
如图所示,长度为L的轻质细杆的一端与质量为m的小球相连,可绕过O点的水平轴自由转动.现在最低点给小球一水平初速度v0,使它能在竖直平面内做圆周运动.设小球在轨道最低点a和最高点b受到细杆的作用力大小分别为F1和F2,重力加速度为g,则下列判断正确的是( )| A. | 若v0>$\sqrt{5gL}$,则v0越大,F1和F2之差越大 | |
| B. | 若v0>$\sqrt{5gL}$,F1和F2之差为定值,与v0的大小无关 | |
| C. | 若v0<$\sqrt{5gL}$,则v0越小,F1和F2之和越小 | |
| D. | 若v0<$\sqrt{5gL}$,F1和F2之和为定值,与v0的大小无关 |
| A. | 开普勒行星运动定律是开普勒在其导师第谷留下的观测记录的基础上整理和研究而来的 | |
| B. | 牛顿对引力常量G进行了准确测定,并于1687年发表在其传世之作《自然哲学的数学原理》中 | |
| C. | 20世纪初,著名物理学家爱因斯坦建立了狭义相对论,狭义相对论指出,质量要随着物体运动速度的增大而增大 | |
| D. | 20世纪的20年代建立了量子力学理论,它使人们认识到经典力学理论一般不适用于微观粒子的运动 |
| A. | 两个系统相互接触而传热,当两个系统的内能相等时就达到了热平衡 | |
| B. | 彩色液晶显示器利用了液晶的光学性质具有各向异性的特点 | |
| C. | 干湿泡温度计的湿泡显示的温度高于干泡显示的温度,这是湿泡外纱布中的水蒸发吸热的结果 | |
| D. | 液体与大气相接触,表面层内分子所受其他分子的作用表现为相互吸引 | |
| E. | 气体分子单位时间内与单位面积器壁碰撞的次数与单位体积内的分子数和温度有关 |
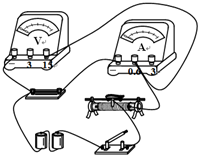 在“测定金属的电阻率”的实验中,用螺旋测微器测出金属丝的直径d,用米尺测出金属丝的长度L,用伏安法测出金属丝的电阻R(金属丝的电阻大约为5Ω).
在“测定金属的电阻率”的实验中,用螺旋测微器测出金属丝的直径d,用米尺测出金属丝的长度L,用伏安法测出金属丝的电阻R(金属丝的电阻大约为5Ω).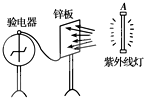 如图所示,一验电器与锌板相连,在A处用一紫外线灯照射锌板,关灯后,指针保持一定偏角.
如图所示,一验电器与锌板相连,在A处用一紫外线灯照射锌板,关灯后,指针保持一定偏角.