题目内容
16.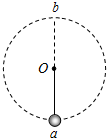 如图所示,长度为L的轻质细杆的一端与质量为m的小球相连,可绕过O点的水平轴自由转动.现在最低点给小球一水平初速度v0,使它能在竖直平面内做圆周运动.设小球在轨道最低点a和最高点b受到细杆的作用力大小分别为F1和F2,重力加速度为g,则下列判断正确的是( )
如图所示,长度为L的轻质细杆的一端与质量为m的小球相连,可绕过O点的水平轴自由转动.现在最低点给小球一水平初速度v0,使它能在竖直平面内做圆周运动.设小球在轨道最低点a和最高点b受到细杆的作用力大小分别为F1和F2,重力加速度为g,则下列判断正确的是( )| A. | 若v0>$\sqrt{5gL}$,则v0越大,F1和F2之差越大 | |
| B. | 若v0>$\sqrt{5gL}$,F1和F2之差为定值,与v0的大小无关 | |
| C. | 若v0<$\sqrt{5gL}$,则v0越小,F1和F2之和越小 | |
| D. | 若v0<$\sqrt{5gL}$,F1和F2之和为定值,与v0的大小无关 |
分析 先根据动能定理求出小球在最高点速度与初速度的关系,分两种情况判断最高点杆子作用力的方向,再在最高点和最低点分别根据向心力公式列式,联立方程求解即可.
解答 解:从最高点到最低点的过程中,根据动能定理得:
$\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}m{v}^{2}=mg•2L$
解得:v=$\sqrt{{{v}_{0}}^{2}-4gL}$
A、当v0>$\sqrt{5gL}$时,则v$>\sqrt{gL}$,则在最高点,杆子提供拉力,则有:
mg+${F}_{2}=m\frac{{v}^{2}}{L}$
解得:${F}_{2}=m\frac{{v}^{2}}{L}-mg=m\frac{{{v}_{0}}^{2}}{L}-5mg$
在最低点,则有:${F}_{1}-mg=m\frac{{{v}_{0}}^{2}}{L}$
解得:${F}_{1}=mg+m\frac{{{v}_{0}}^{2}}{L}$
则F1-F2=6mg,为定值,与v0的大小无关,故A错误,B正确;
C、当v0<$\sqrt{5gL}$时,则$v<\sqrt{gL}$,则杆子提供支持力,在最高点则有:
mg-${F}_{2}=m\frac{{v}^{2}}{L}$
解得:${F}_{2}=mg-m\frac{{v}^{2}}{L}=5mg-m\frac{{{v}_{0}}^{2}}{L}$,
在最低点,则有:${F}_{1}-mg=m\frac{{{v}_{0}}^{2}}{L}$
解得:${F}_{1}=mg+m\frac{{{v}_{0}}^{2}}{L}$
则F1+F2=6mg,为定值,与v0的大小无关,故C错误,D正确;
故选:BD
点评 轻杆的作用力可以提供支持力,也可以提供拉力,要判断是拉力还是支持力,我们要从小球所需要得向心力入手研究,根据需要的向心力的大小和方向确定杆子的作用力.要注意杆与绳子的区别,杆可以是支持力,可以是拉力,而绳子只能为拉力.

 一个匝数为N=100的线圈在匀强磁场中匀速转动,产生的感应电动势的图象如图所示,下列说法正确的是( )
一个匝数为N=100的线圈在匀强磁场中匀速转动,产生的感应电动势的图象如图所示,下列说法正确的是( )| A. | 0.15s时刻,线圈处于与中性面相互垂直的位置 | |
| B. | 0.01s时刻,穿过线圈的磁通量为0 | |
| C. | 线圈转动的角速度为50πrad/s | |
| D. | 穿过线圈的磁通量变化率的最大值为22Wb/s |
| A. | 扩散现象说明物质的分子在做永不停息的无规则运动 | |
| B. | 压缩气体时气体会表现出抗拒压缩的力是由于气体分子间存在斥力的缘故 | |
| C. | 两个分子距离减小时,分子间引力和斥力都在增大 | |
| D. | 两个分子间的距离为r0时,分子势能为0 |
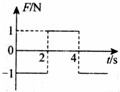 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t变化的图象如图所示,则下列说法中正确的是( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t变化的图象如图所示,则下列说法中正确的是( )| A. | 0~4s内物体的位移为零 | B. | 0~4s内拉力对物体做功为零 | ||
| C. | 4s末物体的动量为零 | D. | 0~4s内拉力对物体冲量为零 |
| A. | 翟志刚需要用很大的力才能把舱盖打开是因为舱内有接近一个大气压的空气压强,而舱外的太空气压为零 | |
| B. | 翟志刚打开舱盖时,轨道舱内有与地表附近相似的空气,但由于完全失重,这些空气产生的气压为零 | |
| C. | 翟志刚打开舱盖前,轨道舱中应该已经过泄压,舱内接近真空 | |
| D. | 翟志刚打开舱盖时,轨道舱内和舱外的太空都有约为一个大气压的空气压强 |
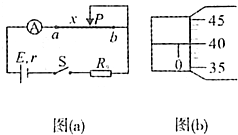
待测的粗细均匀的电阻丝、电流表(量程0.6A,内阻忽略不计)、电源(电动势3.0V,内阻r未知)、保护电阻(R0=4.0Ω)、刻度尺、螺旋测微器、开关S、导线若干、滑片P.
实验步骤如下:
①用螺旋测微器测得电阻丝的直径d如图(b)所示;
②闭合开关,调节滑片P的位置,分别记录每次实验中aP长度x及对应的电流值I;
③以$\frac{1}{I}$为纵坐标,x为横坐标,作$\frac{1}{I}$-x图线(用直线拟合);
④求出直线的斜率k和在纵轴上的截距b.
回答下列问题:
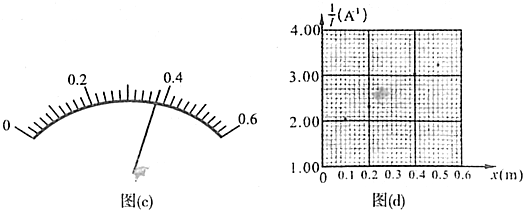
(1)螺旋测微器求数为d=0.400mm.
(2)用题中字母可求得$\frac{1}{I}$与x的关系式为$\frac{1}{I}$=$\frac{4ρ}{πE{d}^{2}}x+\frac{{R}_{0}+r}{E}$.
(3)实验得到的部分数据如表所示,其中aP长度=0.30m时电流表的示数如图(c)所示,读出数据,完成下表,答:①0.38,②2.63.
| x(m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| I(A) | 0.49 | 0.43 | ① | 0.33 | 0.31 | 0.28 |
| $\frac{1}{I}$(A-1) | 2.04 | 2.33 | ② | 3.03 | 3.23 | 3.57 |
(5)根据图线求得电阻丝的电阻率ρ=1.10×10-6,电源的内阻为r=1.30Ω.(保留三位有效数字)
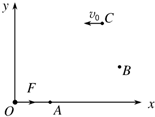 如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、O两点距离为a,在A点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求:
如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、O两点距离为a,在A点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求: 如图所示,在磁感应强度为B,方向竖直向下的匀强磁场中,相距为L的两根足够长平行光滑金属轨道MN、PQ固定在水平面内,一质量为m、电阻为R1的导体棒ab垂直轨道旋转且与轨道电接触良好,轨道左端M点接一单刀双掷开关S,P点与电动势为E,内阻为r的电源和定值R2相连接,不计连轨道的电阻.
如图所示,在磁感应强度为B,方向竖直向下的匀强磁场中,相距为L的两根足够长平行光滑金属轨道MN、PQ固定在水平面内,一质量为m、电阻为R1的导体棒ab垂直轨道旋转且与轨道电接触良好,轨道左端M点接一单刀双掷开关S,P点与电动势为E,内阻为r的电源和定值R2相连接,不计连轨道的电阻.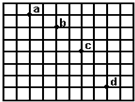 如图所示,在“研究平抛物体的运动”的实验中,用一张印有小方格的纸记录轨迹,小方格的边长为L=1.25cm,若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度v0=0.7m/s (g取9.8m/s2),小球从a运动到d的时间0.1s,d点竖直方向的速率是1m/s.(保留一位有效数字)
如图所示,在“研究平抛物体的运动”的实验中,用一张印有小方格的纸记录轨迹,小方格的边长为L=1.25cm,若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度v0=0.7m/s (g取9.8m/s2),小球从a运动到d的时间0.1s,d点竖直方向的速率是1m/s.(保留一位有效数字)