题目内容
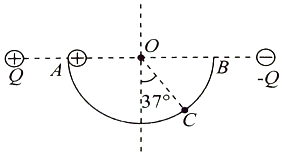
【题目】如图，三角形ABC为某透明介质的横截面，O为BC边的中点，位于截面所在平面内的束光线自O以角入射，第一次到达AB边恰好发生全反射．已知θ=15°，BC边长为2L，该介质的折射率为 
．求：
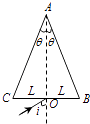
（1）入射角i；
（2）从入射到发生第一次全反射的时间（设光在真空中的速度为c，可能用到sin75°= 
或tan15°=2﹣ 
）
【答案】
（1）解：根据全反射定律可知，光线在AB面上P点的入射角等于临界角C，由折射定律得：
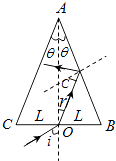
sinC= 
①
代入数据得：C=45° ②
设光线在BC面上的折射角为r，由几何关系得：r=30° ③
由折射定律得：n= 
④
联立③④式，代入数据得：i=45° ⑤
答：入射角i为45°；
（2）解：在△OPB中，根据正弦定理得： 
= 
⑥
设所用时间为t，光线在介质中的速度为v，得： 
=vt ⑦
光在玻璃中的传播速度 v= 
⑧
联立⑥⑦⑧式，代入数据得：t= 
⑨
答：从入射角到发生第一次全反射所用的时间是 ．
【解析】（1）光线在AB面上P点的入射角等于临界角C，根据折射率和临界角之间的关系，求出临界角，在结合题目当中已知的几何关系，利用折射定律求出入射角。
（2）首先利用正玄定理求出发生全反射时走过的距离，利用光在介质中传播的速度和折射率之间的关系，求出光在介质中传播的速度，最后利用匀速直线运动公式，求解光传播的时间。
【考点精析】解答此题的关键在于理解光的折射的相关知识，掌握光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射．
练习册系列答案
相关题目
