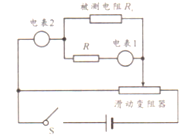
题目内容
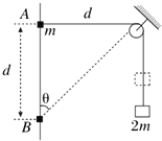
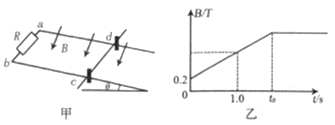
【题目】如图甲所示，两根平行金属导轨固定倾斜放置，与水平面夹角为θ=37°，相距d=1.0m，a、b间接一个阻值R=5.0Ω的电阻，在导轨上c、d两点处放一根质量m=0.1kg的金属棒，bc长为L=4.0m，cd平行ab，金属棒与导轨间的动摩擦因数μ=0.5，金属棒与导轨接触点间电阻r=3.0Ω，导轨电阻忽略不计，金属棒与导轨间的最大静摩擦力等于滑动摩擦力，金属棒被两个垂直于导轨的绝缘桩挡住而不会下滑，在金属导轨区域加一个垂直导轨平面斜向下的匀强磁场，磁场随时间的变化关系如图乙所示已知0~1.0s时间内回路中产生的感应电动势大小E=4.0V，重力加速度g=10m/s2，sin37°=0.6。求：
(1)在t=1.0s时，磁感应强度B的大小；
(2) t=1.0s时，金属棒所受的安培力的大小；
(3)在磁场变化的全过程中，若金属棒始终没有离开绝缘桩而上升，则图乙中t0的最大值；
(4)在t=0.2s时撤去绝缘桩，求0.2s~t0为最大值的时间内，金属棒受到的摩擦力f随时间t变化的关系式。
【答案】(1) 1.2T (2) 0.6N (3) l.8s (4) f=0.5t-0.5
【解析】
(1)根据法拉第电磁感应定律
解得磁感应强度的变化率
=1T/s
0-
时间内有B=0.2+
=0.2+t
解得t=1.0s时，磁感应强度的大小B=1.2T
(2)由闭合电路欧姆定律，在t=l.0s时由于磁场变化产生的感应电流
=0.5A
t=l.0s时，金属棒所受的安培力F0=RId=(0.2+t)Id=0.6N
(3)金属棒始终没有离开绝緣桩而上升，为最大值时，静摩擦力达到最大，且沿斜面向下，沿倾斜导轨方向上合外力为零
Bld=mgsinθ+μmgcosθ
为最大值时I=0.5A，B=0.2+
解得=l.8s
(4)t=0.2s时撤去绝缘桩，金属棒所受的安培力F1=BId=(0.2+t)Id=0.2N此时金属梓恰好不沿金属轨道运动，摩擦力为最大静摩擦力，方向沿轨道平面向上
当金属棒所受的摩擦力为零时，F2=BId=(0.2+t)Id=mgsinθ
可解得t=1.0s
由以上计算可知，在0.2s-1.0s内金属棒所受摩擦力沿斜面向上，且处于静止状态
满足f+(0.2+t)Id=mgsinθ
解得f=0.5-0.5t
在1.0s-1.8s内，金属棒所受摩擦力沿斜面向下，且处于静止状态
满足(0.2+t)Id=mgsinθ+f
解得f=0.5t-0.5
