题目内容
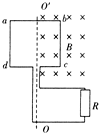
【题目】如图所示，甲、乙两小球位于
的同一高度，零时刻由静止释放甲球，
后再由静止释放乙球，释放后两球均做自由落体运动。（重力加速度
取
），求：
（1）释放乙球时，甲球离地高度.
（2）甲小球落地时，甲、乙两小球之间的竖直距离.
（3）从甲小球下落开始计时，分析全过程甲、乙两球之间的竖直距离与时间的关系，并用图像准确表示。（球落地后立即原地静止）
【答案】（1）40m
（2）25m
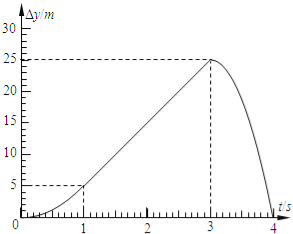
（3）如图所示．
【解析】
试题（1）根据位移时间公式求出甲球1s内下落的高度，从而得出甲球离地的高度．
（2）根据位移时间公式求出甲球落地的时间，从而得出乙球下落的时间，根据位移是公式求出乙球下落的高度，从而得出两球之间的竖直距离．
（3）根据位移时间公式求出各段时间内甲乙两球之间距离的表达式，从而作出图线．
解：（1）释放乙球时，甲下落高度h1=
gt12=
=5m
得甲离地高度△h1=h﹣h1=40m．
（2）由h=gt22，得甲球落地时间t2=
=3s，
此时乙下落高度h2=g（t2﹣1）2=
=20m
所以甲、乙之间的距离△h2=h﹣h2=25m
（3）从甲下落开始计时，甲下落高度y1=
gt2，乙球下落高度y2=g（t﹣1）2，两者之间的高度差△y=y1﹣y2
在0～1s内，y1=gt2，y2=0，两球的竖直距离随时间的关系为△y1=y1﹣y2=gt2=5t2
在1～3s内，y1=gt2，y2=g（t﹣1）2，两小球的竖直距离随时间的关系为：△y2=y1﹣y2=10t﹣5
在3～4s内，y1=45m，y2=g（t﹣1）2，两小球的竖直距离随时间的关系为：△y3=y1﹣y2=40+10t﹣5t2
则图象如图所示．
答：（1）释放乙球时，甲球离地高度为40m．
（2）甲小球落地时，甲、乙两小球之间的竖直距离为25m．
（3）如图所示．
