题目内容
 如图所示,将一个质量为m的带电小球在匀强电场中由静止释放,小球在重力及电场力的作用下沿着与竖直方向成37°做匀加速直线运动.
如图所示,将一个质量为m的带电小球在匀强电场中由静止释放,小球在重力及电场力的作用下沿着与竖直方向成37°做匀加速直线运动.(1)若电场方向未知,求小球所受电场力可能的最小值,此力沿何方向?
(2)若小球所受电场力的大小为0.75mg,试求释放后0.20s内小球通过的路程(取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8).
分析:(1)带电小球在电场中受到重力和电场力作用,从O点自由释放,其运动轨迹为直线,小球所受的合力方向沿此直线方向.运用三角定则分析什么情况下电场力最小,再求出最小值.
(2)小球所受电场力的大小为0.75mg,方向有两种:一种、电场力水平向右,另一种电场力方向与竖直方向成16°.根据牛顿第二定律求出加速度,由运动学公式求解路程.
(2)小球所受电场力的大小为0.75mg,方向有两种:一种、电场力水平向右,另一种电场力方向与竖直方向成16°.根据牛顿第二定律求出加速度,由运动学公式求解路程.
解答:解:(1)解:由题,带电小球的运动轨迹为直线,在电场中受到重力mg和电场力F,其合力必定沿此直线向下,根据三角形定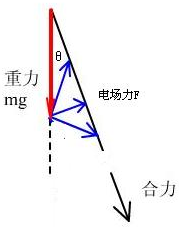 则作出合力,由图看出,当电场力F与此直线垂直时,电场力F最小,最小值为Fmin=mgsinθ,θ=37°得到Fmin=0.6mg.
则作出合力,由图看出,当电场力F与此直线垂直时,电场力F最小,最小值为Fmin=mgsinθ,θ=37°得到Fmin=0.6mg.
(2)本题有两解:
①若电场力水平向右时,小球的加速度为a1=
=12.5m/s2.
由s1=
a1t2得s1=0.25m
②若电场力方向与竖直方向成90°-2×37°=16°时,加速度大小为a2=
=3.5m/s2,由s2=
a2t2得s2=0.07m
答:(1)小球所受电场力可能的最小值为0.6mg,方向与直线垂直向上;
(2)若小球所受电场力的大小为0.75mg,释放后0.20s内小球通过的路程是0.25m或0.07m.
 则作出合力,由图看出,当电场力F与此直线垂直时,电场力F最小,最小值为Fmin=mgsinθ,θ=37°得到Fmin=0.6mg.
则作出合力,由图看出,当电场力F与此直线垂直时,电场力F最小,最小值为Fmin=mgsinθ,θ=37°得到Fmin=0.6mg.(2)本题有两解:
①若电场力水平向右时,小球的加速度为a1=
| ||
| m |
由s1=
| 1 |
| 2 |
②若电场力方向与竖直方向成90°-2×37°=16°时,加速度大小为a2=
| mgcos37°-0.75mgcos53° |
| m |
| 1 |
| 2 |
答:(1)小球所受电场力可能的最小值为0.6mg,方向与直线垂直向上;
(2)若小球所受电场力的大小为0.75mg,释放后0.20s内小球通过的路程是0.25m或0.07m.
点评:本题采用作图法分析场强取得最小值的条件,也可以采用函数法分析电场力与θ的关系,确定最小值的条件.已知电场力大小时,电场力方向不确定,有两种情况,要进行讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
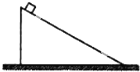 如图所示,将一个质量为1kg的小物块轻轻放在倾角为37°(sin37°=0.6)的斜面上,已知斜面质量也为1kg,重力加速度为10m/s2.若斜面在足够粗糙的水平地面上没有滑动,那么地面的支持力FN和摩擦力Ff有可能为( )
如图所示,将一个质量为1kg的小物块轻轻放在倾角为37°(sin37°=0.6)的斜面上,已知斜面质量也为1kg,重力加速度为10m/s2.若斜面在足够粗糙的水平地面上没有滑动,那么地面的支持力FN和摩擦力Ff有可能为( )| A、FN=16.4N,Ff=4.8N | B、FN=18.2N,Ff=2.4N | C、FN=20N,Ff=0 | D、FN=20N,Ff=4.8N |
 (2012?白银模拟)右端连有光滑弧形槽的水平桌面AB长L=1.5m,如图所示.将一个质量为m=0.5kg的木块在F=1.5N的水平拉力作用下,从桌面上的A端由静止开始向右运动,木块到达B端时撤去拉力F,木块与水平桌面间的动摩擦因数μ=0.2,取g=10m/s2.求:
(2012?白银模拟)右端连有光滑弧形槽的水平桌面AB长L=1.5m,如图所示.将一个质量为m=0.5kg的木块在F=1.5N的水平拉力作用下,从桌面上的A端由静止开始向右运动,木块到达B端时撤去拉力F,木块与水平桌面间的动摩擦因数μ=0.2,取g=10m/s2.求: (2012?洛阳模拟)如图所示,将一个质量为m的球固定在弹性杆AB的上端,今用测力计沿水平方向缓慢拉球,使杆发生弯曲,在测力计的示数逐渐增大的过程中,AB杆对球的弹力方向为( )
(2012?洛阳模拟)如图所示,将一个质量为m的球固定在弹性杆AB的上端,今用测力计沿水平方向缓慢拉球,使杆发生弯曲,在测力计的示数逐渐增大的过程中,AB杆对球的弹力方向为( )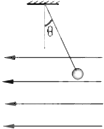 如图所示,将一个质量为m,电量为q的带电小球用绝缘丝线悬挂在O点,小球处在水平方向的匀强电场中.当带电小球达到平衡后,丝线与竖直方向间的夹角为θ.
如图所示,将一个质量为m,电量为q的带电小球用绝缘丝线悬挂在O点,小球处在水平方向的匀强电场中.当带电小球达到平衡后,丝线与竖直方向间的夹角为θ.