题目内容
(20分) 如图所示,两物块A、B并排静置于高h=0.80m的光滑水平桌面上,两物块的质量均为M=0.60kg。一颗质量m=0.10kg的子弹C以v0=100m/s的水平速度从左面射入A物块,子弹射穿A后接着射入B并留在B中,此时A、B都没有离开桌面。已知物块A的长度为0.27m,A离开桌面后,落地点到桌边的水平距离s=2.0m。设子弹在物块A、B 中穿行时受到的阻力保持不变,g取10m/s2。求:
(1)物块A和物块B离开桌面时速度的大小分别是多少;
(2)求子弹在物块B中穿行的距离;
(3)为了使子弹在物块B中穿行时物块B未离开桌面,求物块B到桌边的最小距离。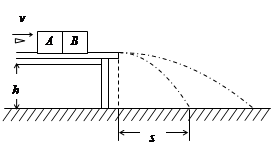
(1)物块A和物块B离开桌面时速度的大小分别是多少;
(2)求子弹在物块B中穿行的距离;
(3)为了使子弹在物块B中穿行时物块B未离开桌面,求物块B到桌边的最小距离。

(1)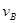 =10m/s(2)
=10m/s(2)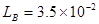 m(3)smin=2.5×10-2m
m(3)smin=2.5×10-2m
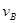 =10m/s(2)
=10m/s(2)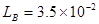 m(3)smin=2.5×10-2m
m(3)smin=2.5×10-2m(1)子弹射穿物块A后,A以速度vA沿桌面水平向右匀速运动,离开桌面后做平抛运动 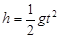 t=0.40s
t=0.40s
A离开桌边的速度
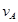 =5.0m/s
=5.0m/s
设子弹射入物块B后,子弹与B的共同速度为vB,子弹与两物块作用过程系统动量守恒:
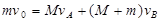
B离开桌边的速度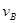 =10m/s
=10m/s
(2)设子弹离开A时的速度为 ,子弹与物块A作用过程系统动量守恒:
,子弹与物块A作用过程系统动量守恒:
 m/s
m/s
子弹在物块B中穿行的过程中,由能量守恒
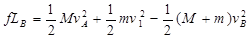 ①
①
子弹在物块A中穿行的过程中,由能量守恒
 ②
②
由①②解得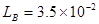 m
m
(3)子弹在物块A中穿行的过程中,物块A在水平桌面上的位移为s1,根据动能定理
 ③
③
子弹在物块B中穿行的过程中,物块B在水平桌面上的位移为s2,根据动能定理

④
由②③④解得物块B到桌边的最小距离 smin=2.5×10-2m
smin=2.5×10-2m
本题考查动量守恒与能量守恒的应用,物块A被子弹射穿后做平抛运动飞出桌面,由平抛运动规律可求得平抛运动的初速度及子弹射穿后木块的速度,在子弹射穿木块过程中系统动量守恒,子弹射进木块B中,木块B向右加速,使得A、B分离,如果以子弹、木块A、B为一个系统,内力远远大于外力,系统动量始终守恒,初状态为AB静止,末状态为子弹与B共速,列式可求得B的速度,再以子弹和木块A为研究对象,动量守恒可求得子弹飞出后的速度,此时AB速度相同,再以子弹和B为一个系统,系统动能的减小量完全转化为内能,系统的内能为阻力乘以相对距离及打进物体B的深度,由此可求解
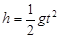 t=0.40s
t=0.40sA离开桌边的速度

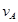 =5.0m/s
=5.0m/s设子弹射入物块B后,子弹与B的共同速度为vB,子弹与两物块作用过程系统动量守恒:
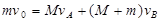
B离开桌边的速度
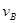 =10m/s
=10m/s(2)设子弹离开A时的速度为
 ,子弹与物块A作用过程系统动量守恒:
,子弹与物块A作用过程系统动量守恒:
 m/s
m/s子弹在物块B中穿行的过程中,由能量守恒
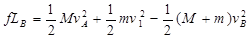 ①
①子弹在物块A中穿行的过程中,由能量守恒
 ②
②由①②解得
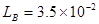 m
m(3)子弹在物块A中穿行的过程中,物块A在水平桌面上的位移为s1,根据动能定理
 ③
③子弹在物块B中穿行的过程中,物块B在水平桌面上的位移为s2,根据动能定理

④
由②③④解得物块B到桌边的最小距离
 smin=2.5×10-2m
smin=2.5×10-2m本题考查动量守恒与能量守恒的应用,物块A被子弹射穿后做平抛运动飞出桌面,由平抛运动规律可求得平抛运动的初速度及子弹射穿后木块的速度,在子弹射穿木块过程中系统动量守恒,子弹射进木块B中,木块B向右加速,使得A、B分离,如果以子弹、木块A、B为一个系统,内力远远大于外力,系统动量始终守恒,初状态为AB静止,末状态为子弹与B共速,列式可求得B的速度,再以子弹和木块A为研究对象,动量守恒可求得子弹飞出后的速度,此时AB速度相同,再以子弹和B为一个系统,系统动能的减小量完全转化为内能,系统的内能为阻力乘以相对距离及打进物体B的深度,由此可求解

练习册系列答案
相关题目