题目内容
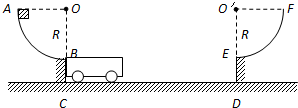
如图所示,固定在地面上的光滑圆弧轨道AB、EF,他们的圆心角均为90°,半径均为R.一质量为m,上表面长也为R的小车静止在光滑水平面CD上,小车上表面与轨道AB、EF的末端B、E相切.一质量为m的物体(大小不计)从轨道AB的A点由静止下滑,由末端B滑上小车,小车在摩擦力的作用下向右运动.当小车右端与壁DE刚接触时,物体m恰好滑动到小车右端且与小车共速.小车与DE相碰后立即停止运动但不粘连,物体则继续滑上圆弧轨道EF,以后又滑下来冲上小车.求:
(1)物体从A点滑到B点时的速率;
(2)物体与小车之间的滑动摩擦力;
(3)水平面CD的长度;
(4)当物体再从轨道EF滑下并滑上小车后,如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端的距离.

(1)物体从A点滑到B点时的速率;
(2)物体与小车之间的滑动摩擦力;
(3)水平面CD的长度;
(4)当物体再从轨道EF滑下并滑上小车后,如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端的距离.
分析:(1)根据机械能守恒定律求出物体从A点滑到B点时的速率;
(2)根据动量守恒定律求出物体滑上小车后的共同速度.对物体和小车组成的系统,运用能量守恒定律列式求解物体与小车之间的滑动摩擦力;
(3)对物体运用动能定理,联立求出水平面CD的长度.
(4)根据动量守恒定律求出AB的共同速度,对系统运用能量守恒定律求出两者速度相同时,之间的相对距离,小车停止后,物体做匀减速直线运动,再根据动能定理求出匀减速直线运动的位移,从而得出最终物体在小车上滑行的距离.
(2)根据动量守恒定律求出物体滑上小车后的共同速度.对物体和小车组成的系统,运用能量守恒定律列式求解物体与小车之间的滑动摩擦力;
(3)对物体运用动能定理,联立求出水平面CD的长度.
(4)根据动量守恒定律求出AB的共同速度,对系统运用能量守恒定律求出两者速度相同时,之间的相对距离,小车停止后,物体做匀减速直线运动,再根据动能定理求出匀减速直线运动的位移,从而得出最终物体在小车上滑行的距离.
解答:解:(1)由机械能守恒定律得:mgR=
mv2
解得:v=
(2)由动量守恒定律得:mv=2mv共
f?R=
mv2-
?2m
解得:f=
mg
(3)对物体:-f?xCD=
m
-
mv2
(或对小车列式:f?(xCD-R)=
m
-0)
解得:xCD=
R
(4)物体从EF滑下后与车共速的速度为v′共,产生的相对位移为s1:
mv共=2mv′共
f?s1=
m
-
?2mv
s1=
R
车撞BC后,物体做匀减速运动的位移为s2:
对物体:-f?s2=0-
mv
s2=
R
Q点距小车右端的距离s=
R+
R=
R
答:(1)物体从A点滑到B点时的速率为
;
(2)物体与小车之间的滑动摩擦力为
mg;
(3)水平面CD的长度为
R;
(4)Q点距小车右端的距离为
R.
| 1 |
| 2 |
解得:v=
| 2gR |
(2)由动量守恒定律得:mv=2mv共
f?R=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 共 |
解得:f=
| 1 |
| 2 |
(3)对物体:-f?xCD=
| 1 |
| 2 |
| v | 2 共 |
| 1 |
| 2 |
(或对小车列式:f?(xCD-R)=
| 1 |
| 2 |
| v | 2 共 |
解得:xCD=
| 3 |
| 2 |
(4)物体从EF滑下后与车共速的速度为v′共,产生的相对位移为s1:
mv共=2mv′共
f?s1=
| 1 |
| 2 |
| v | 2 共 |
| 1 |
| 2 |
| ′ | 2 共 |
| 1 |
| 4 |
车撞BC后,物体做匀减速运动的位移为s2:
对物体:-f?s2=0-
| 1 |
| 2 |
| ′ | 2 共 |
| 1 |
| 8 |
Q点距小车右端的距离s=
| 1 |
| 4 |
| 1 |
| 8 |
| 3 |
| 8 |
答:(1)物体从A点滑到B点时的速率为
| 2gR |
(2)物体与小车之间的滑动摩擦力为
| 1 |
| 2 |
(3)水平面CD的长度为
| 3 |
| 2 |
(4)Q点距小车右端的距离为
| 3 |
| 8 |
点评:本题综合考查了动量守恒定律、能量守恒定律、机械能守恒定律、动能定理,综合性较强,涉及的过程较多,关键是合理地选择研究对象和研究过程,选择合适的规律进行求解.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
如图所示,固定在地面上的光滑斜面顶端固定一弹簧.一物体向右滑行,冲上斜面并压缩弹簧.设物体通过斜面最低点A时的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则弹簧被压缩至最短时具有的弹性势能为

|
C.-mgh D.-(mgh+mv2)
 如图所示,固定在地面上的光滑斜面顶端固定一弹簧.一物体向右滑行,冲上斜面并压缩弹簧.设物体通过斜面最低点A时的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则弹簧被压缩至最短时具有的弹性势能为 ( )
如图所示,固定在地面上的光滑斜面顶端固定一弹簧.一物体向右滑行,冲上斜面并压缩弹簧.设物体通过斜面最低点A时的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则弹簧被压缩至最短时具有的弹性势能为 ( ) 如图所示,固定在匀强磁场中的水平导轨ab、cd的间距L1=0.5m,金属棒ad与导轨左端bc的距离L2=0.8m,整个闭合回路的电阻为R=0.2Ω,匀强磁场的方向竖直向下穿过整个回路.ad杆通过细绳跨过定滑轮接一个质量m=0.04kg的物体,不计一切摩擦.现使磁感应强度从零开始以
如图所示,固定在匀强磁场中的水平导轨ab、cd的间距L1=0.5m,金属棒ad与导轨左端bc的距离L2=0.8m,整个闭合回路的电阻为R=0.2Ω,匀强磁场的方向竖直向下穿过整个回路.ad杆通过细绳跨过定滑轮接一个质量m=0.04kg的物体,不计一切摩擦.现使磁感应强度从零开始以
