题目内容
(18分)如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与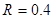 m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以
m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以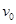 =7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求:
=7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求:
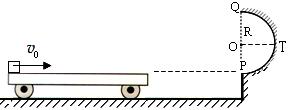
(1)小车与墙壁碰撞前的速度大小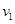 ;
;
(2)小车需要满足的长度L;
(3)请判断滑块能否经过圆轨道的最高点Q,说明理由。
【答案】
(1)5m/s(2)3.75m(3)能
【解析】(1)设滑块与小车的共同速度为v1,滑块与小车相对运动过程中动量守恒,有:
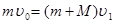 ……………………………………………(2分)
……………………………………………(2分)
代入数据解得: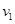 =5m/s …………………………………………………(2分)
=5m/s …………………………………………………(2分)
(2)设小车的最小长度为L1,由系统能量守恒定律,有:
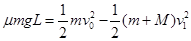 ……………………………………………(2分)
……………………………………………(2分)
代入数据解得:L= 3.75m ………………………………………………………(2分)
(3)若滑块恰能滑过圆的最高点的速度为v,则有:
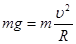 ………………………………………………………………(2分)
………………………………………………………………(2分)
解得: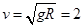 m/s …………………………………………………………(2分)
m/s …………………………………………………………(2分)
滑块从P运动到Q的过程,根据机械能守恒定律,有:
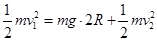 ……………………………………………………(2分)
……………………………………………………(2分)
代入数据解得: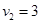 m/s ……………………………………………………(2分)
m/s ……………………………………………………(2分)
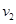 >
>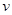 ,说明滑块能过最高点Q。……………………………………………(2分)
,说明滑块能过最高点Q。……………………………………………(2分)

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目

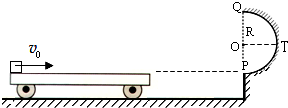 如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与
如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与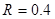 m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以
m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以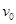 =7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求:
=7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求: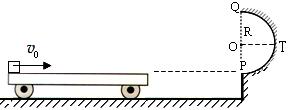
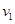 ;
;