题目内容
如图,水平地面和半圆轨道面均光滑,质量为 m 的小车静止在地面上,小车上表面与半径为 R 的半圆轨道最低点 P 切线相平,质量为 mB 的物体 B 静止在 P 点.现有一质量为 mA 的物体 A 以初速度 v0 滑上小车左端,当 A 与小车共速时,小车还未与墙 壁碰撞,小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数为 μ,mA=mB=m,物体 A、B 可视为质点,重力加速度为 g.试求:
(1)物体 A 与小车共速时的速度大小;
(2)小车的最小长度 L;
(3)当物体 A 与 B 发生弹性碰撞后,欲使 B 碰后在圆轨道运动时不脱离圆轨道,小车的长度 L应在什么范围内.

(1)物体 A 与小车共速时的速度大小;
(2)小车的最小长度 L;
(3)当物体 A 与 B 发生弹性碰撞后,欲使 B 碰后在圆轨道运动时不脱离圆轨道,小车的长度 L应在什么范围内.

分析:物体A在小车上面运动,把小车与物体A看做一系统,合外力为零,满足动量守恒列出等式求解
若滑块恰能滑过圆的最高点,由重力提供向心力,由牛顿第二定律求出滑块经过最高点时的速度,根据动能定理求出轨道半径;若滑块恰好滑至
圆弧到达T点时就停止,滑块也能沿圆轨道运动而不脱离圆轨道.根据动能定理求解小车的长度,即能得到小车的长度的范围.
若滑块恰能滑过圆的最高点,由重力提供向心力,由牛顿第二定律求出滑块经过最高点时的速度,根据动能定理求出轨道半径;若滑块恰好滑至
| 1 |
| 4 |
解答:解:(1)物体A在小车上面运动,把小车与物体A看做一系统,合外力为零,满足动量守恒,
有:mAV0=(mA+mB)V共且mA=mB=m
解得V共=
v0
(2)若问题A与小车达到共同速度时,恰好运动到小车的右端,此情况下小车的长度是最小长度,
由系统动能定理得
-μmAgL=
(mA+m)
-
mA
解得L=
(3)假设问题A与小车达到共同速度时,距离小车的右端为S,小车粘到墙壁上之后,
物体A开始匀减速直线运动,直到P点是速度为vt,
由动能定理得:
-μmAgS=
mA
-
mA
得出:
mA
=
mA
-μmAgS
①欲保证A能滑到P点,vt≥0
mA
-μmAgS≥0
S≤
,此情况下小车的长度L总=L+S=
②A能滑到P点与B发生弹性碰撞,满足动量和动能守恒,
mAvt=mAvA+mBvB
解得:vA=0,vB=vt
以后B做圆周运动,恰能运动到最高点,
在最高点速度vB0=
根据机械能守恒有
mBg?2R+
mB
=
mB
解得:S=
-
此情况下小车的长度L总=L+S=
-
③如果滑块滑到
圆滑就停止,滑块也能沿圆轨道运动而不脱离圆轨道根据机械能守恒有
mBgR=
mB
S═
-
此情况下小车的长度L总=L+S=
-
综上所述,滑块能沿圆轨道运动而不脱离圆轨道,半圆轨道的半径必须满足:
<L≤
-
或=
-
≤L≤
答:(1)物体 A 与小车共速时的速度大小是
v0;
(2)小车的最小长度是
;
(3)当物体 A 与 B 发生弹性碰撞后,欲使 B 碰后在圆轨道运动时不脱离圆轨道,
小车的长度 L范围是
<L≤
-
或
-
≤L≤
.
有:mAV0=(mA+mB)V共且mA=mB=m
解得V共=
| 1 |
| 2 |
(2)若问题A与小车达到共同速度时,恰好运动到小车的右端,此情况下小车的长度是最小长度,
由系统动能定理得
-μmAgL=
| 1 |
| 2 |
| v | 2 共 |
| 1 |
| 2 |
| v | 2 0 |
解得L=
| ||
| 4μg |
(3)假设问题A与小车达到共同速度时,距离小车的右端为S,小车粘到墙壁上之后,
物体A开始匀减速直线运动,直到P点是速度为vt,
由动能定理得:
-μmAgS=
| 1 |
| 2 |
| v | 2 t |
| 1 |
| 2 |
| v | 2 共 |
得出:
| 1 |
| 2 |
| v | 2 t |
| 1 |
| 8 |
| v | 2 0 |
①欲保证A能滑到P点,vt≥0
| 1 |
| 8 |
| v | 2 0 |
S≤
| ||
| 8μg |
| ||
| 8μg |
②A能滑到P点与B发生弹性碰撞,满足动量和动能守恒,
mAvt=mAvA+mBvB
解得:vA=0,vB=vt
以后B做圆周运动,恰能运动到最高点,
在最高点速度vB0=
| gR |
根据机械能守恒有
mBg?2R+
| 1 |
| 2 |
| v | 2 BO |
| 1 |
| 2 |
| v | 2 t |
解得:S=
| ||
| 8μg |
| 5R |
| 2μ |
此情况下小车的长度L总=L+S=
| ||
| 8μg |
| 5R |
| 2μ |
③如果滑块滑到
| 1 |
| 4 |
mBgR=
| 1 |
| 2 |
| v | 2 t |
S═
| ||
| 8μg |
| R |
| μ |
此情况下小车的长度L总=L+S=
| ||
| 8μg |
| R |
| μ |
综上所述,滑块能沿圆轨道运动而不脱离圆轨道,半圆轨道的半径必须满足:
| ||
| 4μg |
| ||
| 8μg |
| 5R |
| 2μ |
或=
| ||
| 8μg |
| R |
| μ |
| ||
| 8μg |
答:(1)物体 A 与小车共速时的速度大小是
| 1 |
| 2 |
(2)小车的最小长度是
| ||
| 4μg |
(3)当物体 A 与 B 发生弹性碰撞后,欲使 B 碰后在圆轨道运动时不脱离圆轨道,
小车的长度 L范围是
| ||
| 4μg |
| ||
| 8μg |
| 5R |
| 2μ |
或
| ||
| 8μg |
| R |
| μ |
| ||
| 8μg |
点评:本题通过计算分析小车与墙壁碰撞前滑块与小车的速度是否相同是难点.第3题容易只考虑滑块通过最高点的情况,而遗漏滑块恰好滑至
圆弧到达T点时停止的情况,要培养自己分析隐含的临界状态的能力.
| 1 |
| 4 |

练习册系列答案
相关题目
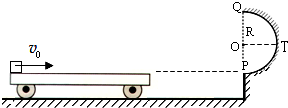 如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与
如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与 m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以
m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以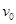 =7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求:
=7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求:
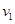 ;
;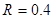 m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以
m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以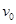 =7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求:
=7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求: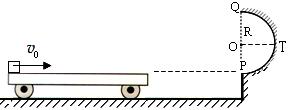
 ;
;