题目内容
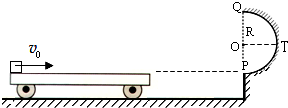 如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与t1=
如图,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与t1=| R | ||
|
2
| ||
| 3qB |
| ||||
| υ |
| πm |
| 3qB |
(1)求小车的最小长度.
(2)讨论小车的长度L在什么范围,滑块能滑上P点且在圆轨道运动时不脱离圆轨道?
分析:(1)滑块在小车滑行过程,系统所受的合外力为零,动量守恒,可求出共同速度.小车的长度与系统产生的内能有关.当两者速度相同滑块刚好滑到小车的右端时,小车的长度最短,根据能量守恒求解最小长度;
(2)滑块不脱离圆轨道可能从Q点离开轨道,也可能滑到T点,根据动能定理结合上题的结果可求出L的范围.
(2)滑块不脱离圆轨道可能从Q点离开轨道,也可能滑到T点,根据动能定理结合上题的结果可求出L的范围.
解答:解:(1)设滑块与小车的共同速度为v1,滑块与小车相对运动过程中动量守恒,有:
mυ0=(m+M)υ1
代入数据解得:υ1=4m/s
设小车的最小长度为L1,由系统能量守恒定律,有:
μmgL 1=
mυ 0 2-
(m+M)υ1 2
代入数据解得:L1=3m
(2)设小车与墙壁碰撞时,滑块与P点的距离为L2,若滑块恰能滑过圆的最高点,
设滑至最高点的速度为v,临界条件为:mg=m
…①
根据动能定理,有:-μmgL 2-mg?2R=
mυ 2-
mυ 1 2…②
①②联立并代入数据解得:L2=1m
这种情况下小车的长度为:L=L1+L2=4m
若滑块恰好滑至
圆弧到达T点时就停止,则滑块也能沿圆轨道运动而不脱离圆轨道.
根据动能定理,有:-μmgL 2-mg?R=0-
mυ 1 2
代入数据解得:L2=2.8m
这种情况下小车的长度为:L=L1+L2=5.8m
若滑块滑至P点时速度恰好为零,由动能定理,有:-μmgL2=0-
m
解得:L2=4m
这种情况下小车的长度为:L=L1+L2=7m
综上所述,滑块能沿圆轨道运动而不脱离圆轨道,半圆轨道的半径必须满足:3m≤L≤4m或5.8m≤L<7m
答:(1)小车的最小长度为3m;
(2)小车的长度L在3m≤L≤4m或3m≤L≤5.8m范围,滑块能滑上P点且在圆轨道运动时不脱离圆轨道.
mυ0=(m+M)υ1
代入数据解得:υ1=4m/s
设小车的最小长度为L1,由系统能量守恒定律,有:
μmgL 1=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:L1=3m
(2)设小车与墙壁碰撞时,滑块与P点的距离为L2,若滑块恰能滑过圆的最高点,
设滑至最高点的速度为v,临界条件为:mg=m
| υ 2 |
| R |
根据动能定理,有:-μmgL 2-mg?2R=
| 1 |
| 2 |
| 1 |
| 2 |
①②联立并代入数据解得:L2=1m
这种情况下小车的长度为:L=L1+L2=4m
若滑块恰好滑至
| 1 |
| 4 |
根据动能定理,有:-μmgL 2-mg?R=0-
| 1 |
| 2 |
代入数据解得:L2=2.8m
这种情况下小车的长度为:L=L1+L2=5.8m
若滑块滑至P点时速度恰好为零,由动能定理,有:-μmgL2=0-
| 1 |
| 2 |
| υ | 2 1 |
解得:L2=4m
这种情况下小车的长度为:L=L1+L2=7m
综上所述,滑块能沿圆轨道运动而不脱离圆轨道,半圆轨道的半径必须满足:3m≤L≤4m或5.8m≤L<7m
答:(1)小车的最小长度为3m;
(2)小车的长度L在3m≤L≤4m或3m≤L≤5.8m范围,滑块能滑上P点且在圆轨道运动时不脱离圆轨道.
点评:当遇到相互作用的问题时要想到运用动量守恒定律并结合能量守恒定律求解,当遇到竖直面内圆周运动问题时注意临界速度的求法.该题还要注意对滑块能沿圆轨道运动而不脱离圆轨道的情景分析.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目

 m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以
m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以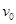 =7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求:
=7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求: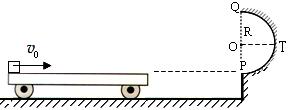
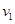 ;
;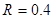 m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以
m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以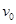 =7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求:
=7.5m/s的初速度滑上小车左端,二者共速时滑块刚好在小车的最右边缘,此时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,滑块则离开小车进入圆轨道并顺着圆轨道往上运动,已知滑块与小车表面的滑动摩擦因数μ=0.5,g取10m/s2.求: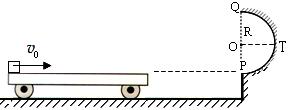
 ;
;