题目内容
3．平抛一物体，落地时速度方向与水平方向的夹角为θ．取地面为重力势能参考平面，则物体被抛出时，其重力势能和动能之比为（ ）| A． | tanθ | B． | cotθ | C． | cot2θ | D． | tan2θ |
分析 由于落地速度与水平方向的夹角已知，假设末速度为v，则可以求出平抛的初速度和初位置的高度，表示出动能与势能，从而得出结果．
解答 解：设物体抛出点的高度为h，初速度为v0，则落地时速度为v=v0/cosθ，平抛过程只有重力做功，物体机械能守恒，得：
mgh+$\frac{1}{2}$mv02=$\frac{1}{2}$mv2=$\frac{1}{2}$m$\frac{{v}_{0}^{2}}{co{s}^{2}θ}$，
所以有：mgh=$\frac{1}{2}$mv02•tan2θ．
重力势能和动能之比为tan2θ
故选：D
点评 本题关键根据末速度的大小和方向，求解出抛出时的动能和势能的表达式，再求得比值即可．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
5．下列说法正确的是（ ）
| A． | 物体做曲线运动时，加速度一定不为零 | |
| B． | 两个直线运动的合运动一定是直线运动 | |
| C． | 平抛是匀变速曲线运动 | |
| D． | 匀速的圆周运动的线速度是不变的 |
2．
如图所示，水平桌面上的轻质弹簧一端固定，另一端与小物块相连．弹簧处于自然长度时物块位于O点（图中未标出）．物块的质量为m，AB=a，物块与桌面间的动摩擦因数为μ．现用水平向右的力将物块从O点拉至A点，拉力做的功为W．撤去拉力后物块由静止向左运动，经O点到达B点时速度为零．重力加速度为g．则上述过程中（ ）
如图所示，水平桌面上的轻质弹簧一端固定，另一端与小物块相连．弹簧处于自然长度时物块位于O点（图中未标出）．物块的质量为m，AB=a，物块与桌面间的动摩擦因数为μ．现用水平向右的力将物块从O点拉至A点，拉力做的功为W．撤去拉力后物块由静止向左运动，经O点到达B点时速度为零．重力加速度为g．则上述过程中（ ）| A． | 物块在A点时，弹簧的弹性势能等于W-$\frac{μmga}{2}$ | |
| B． | 物块在B点时，弹簧的弹性势能小于W-$\frac{3μmga}{2}$ | |
| C． | 物块经O点时，物块的动能等于W-μmga | |
| D． | 物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能 |
某模型汽车的质量为2kg，在水平面上做测试时，先以恒定牵引力F=12N从静止开始做匀加速运动，10s末速度达到10m/s时，发动机功率恰好达到最大值．从该时刻起，汽车保持该最大功率继续加速，经历一段时间后，汽车达到了最大速度．上述过程模型汽车的v-t图象如图所示．由以上信息可知：模型汽车牵引力的最大功率Pm=120W；模型汽车做匀加速运动阶段的加速度大小为a=1m/s2；本次测试的前20s内汽车牵引力做的功为W=1800J．
图为用电源、电磁继电器、滑动变阻器、绿灯泡、小电铃、半导体热敏电阻、开关、导线等组成的一个高温报警器电路图，要求是：正常情况绿灯亮，有险情时电铃报警，则图中的甲是半导体热敏电阻；乙是小电铃；丙是绿灯泡．
12．
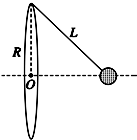在竖直平面内固定一半径为R的金属细圆环，质量为m的金属小球（视为质点）通过长为L的绝缘细线悬挂在圆环的最高点．当圆环、小球都带有相同的电荷量Q（未知）时，发现小球在垂直圆环平面的对称轴上处于平衡状态，如图所示．已知静电力常量为k．则下列说法中正确的是（ ）
在竖直平面内固定一半径为R的金属细圆环，质量为m的金属小球（视为质点）通过长为L的绝缘细线悬挂在圆环的最高点．当圆环、小球都带有相同的电荷量Q（未知）时，发现小球在垂直圆环平面的对称轴上处于平衡状态，如图所示．已知静电力常量为k．则下列说法中正确的是（ ）| A． | 电荷量Q=$\sqrt{\frac{mg{L}^{3}}{kR}}$ | B． | 电荷量Q=$\sqrt{\frac{mg（{L}^{2}-{R}^{2}）{L}^{\frac{3}{2}}}{kR}}$ | ||
| C． | 线对小球的拉力F=$\frac{mgL}{R}$ | D． | 线对小球的拉力F=$\frac{mgR}{\sqrt{{L}^{2}-{R}^{2}}}$ |
