题目内容
12.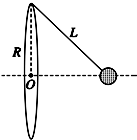 在竖直平面内固定一半径为R的金属细圆环,质量为m的金属小球(视为质点)通过长为L的绝缘细线悬挂在圆环的最高点.当圆环、小球都带有相同的电荷量Q(未知)时,发现小球在垂直圆环平面的对称轴上处于平衡状态,如图所示.已知静电力常量为k.则下列说法中正确的是( )
在竖直平面内固定一半径为R的金属细圆环,质量为m的金属小球(视为质点)通过长为L的绝缘细线悬挂在圆环的最高点.当圆环、小球都带有相同的电荷量Q(未知)时,发现小球在垂直圆环平面的对称轴上处于平衡状态,如图所示.已知静电力常量为k.则下列说法中正确的是( )| A. | 电荷量Q=$\sqrt{\frac{mg{L}^{3}}{kR}}$ | B. | 电荷量Q=$\sqrt{\frac{mg({L}^{2}-{R}^{2}){L}^{\frac{3}{2}}}{kR}}$ | ||
| C. | 线对小球的拉力F=$\frac{mgL}{R}$ | D. | 线对小球的拉力F=$\frac{mgR}{\sqrt{{L}^{2}-{R}^{2}}}$ |
分析 小球受到的库仑力为圆环各点对小球库仑力的合力,则取圆环上△x来分析,再取以圆心对称的△x,这2点合力向右,距离L,竖直方向抵消,只有水平方向;求所有部分的合力Σ△m,即可求得库仑力的表达式;小球受重力、拉力及库仑力而处于平衡,则由共点力的平衡条件可求得绳对小球的拉力及库仑力;则可求得电量.
解答 解:由于圆环不能看作点电荷,我们取圆环上一部分△x,设总电量为Q,则该部分电量为$\frac{△x}{2πR}$Q;
由库仑定律可得,该部分对小球的库仑力F1=$\frac{KQ△XQ}{2π{L}^{2}R}$,方向沿该点与小球的连线指向小球;
同理取以圆心对称的相同的一段,其库仑力与F1相同;如图所示,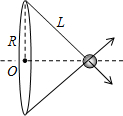
两力的合力应沿圆心与小球的连线向外,大小为2$\frac{KQ△XQ}{2π{L}^{2}R}$×$\frac{\sqrt{{L}^{2}-{R}^{2}}}{L}$=$\frac{K{Q}^{2}△X}{π{L}^{3}R}\sqrt{{L}^{2}-{R}^{2}}$;
因圆环上各点对小球均有库仑力,故所有部分库仑力的合力F库=$\frac{K{Q}^{2}\sqrt{{L}^{2}-{R}^{2}}}{π{L}^{3}R}$×πR=$\frac{K{Q}^{2}}{{L}^{3}}\sqrt{{L}^{2}-{R}^{2}}$,方向水平向右;
小球受力分析如图所示,小球受重力、拉力及库仑力而处于平衡,故T与F的合力应与重力大小相等,方向相反;
由几何关系可得:$\frac{T}{L}$=$\frac{mg}{R}$;
则小球对绳子的拉力T=$\frac{mgL}{R}$;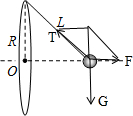
$\frac{F}{\sqrt{{L}^{2}-{R}^{2}}}$=$\frac{mg}{R}$;
则F=$\frac{mg}{R}\sqrt{{L}^{2}-{R}^{2}}$=$\frac{K{Q}^{2}}{{L}^{3}}\sqrt{{L}^{2}-{R}^{2}}$;
解得Q=$\sqrt{\frac{mg{L}^{3}}{kR}}$; 故AC正确,BD错误;
故选:AC.
点评 因库仑定律只能适用于真空中的点电荷,故本题采用了微元法求得圆环对小球的库仑力,应注意体会该方法的使用.
库仑力的考查一般都是结合共点力的平衡进行的,应注意正确进行受力分析.

| A. | tanθ | B. | cotθ | C. | cot2θ | D. | tan2θ |
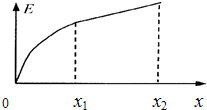 在某集装箱码头上,一架起重机将放在地面上的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中0~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )
在某集装箱码头上,一架起重机将放在地面上的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中0~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )| A. | 0~x1过程中钢绳的拉力逐渐增大 | |
| B. | 0~x1过程中箱子的动能一直增加 | |
| C. | x1~x2过程中钢绳的拉力一直不变 | |
| D. | x1~x2过程中起重机的输出功率一直增大 |
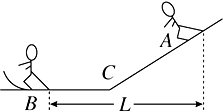 如图所示,滑雪者由静止开始沿斜坡从A点自由滑下,然后在水平面上前进至B点停下.已知斜坡、水平面与滑雪板之间的动摩擦因数都为2μ,滑雪者(包括滑雪板)的质量为3m.A、B两点间的水平距离为L.在滑雪者经过AB段运动的过程中,克服摩擦力做的功为( )
如图所示,滑雪者由静止开始沿斜坡从A点自由滑下,然后在水平面上前进至B点停下.已知斜坡、水平面与滑雪板之间的动摩擦因数都为2μ,滑雪者(包括滑雪板)的质量为3m.A、B两点间的水平距离为L.在滑雪者经过AB段运动的过程中,克服摩擦力做的功为( )| A. | μmgL | B. | 5μmgL | ||
| C. | 6μmgL | D. | 以上三种情况都有可能 |
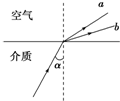
| A. | 逐渐增大入射角α的过程中,a光先发生全反射 | |
| B. | 在该介质中b光的传播速度大于a光的传播速度 | |
| C. | 在该介质中a光的波长小于b光的波长 | |
| D. | 通过同一双缝干涉装置,a光的干涉条纹间距比b光的宽 |
| A. | 机械波和电磁波都能发生反射、折射、干涉和衍射现象,而且它们都可以在真空中传播 | |
| B. | 变化的电场一定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| C. | 电磁波是横波 | |
| D. | 麦克斯韦预言了电磁波的存在并通过实验进行了验证 |
| A. | 若移去检验电荷,该点的电场强度变为零 | |
| B. | 若在该点放一个电量为2q的检验电荷,该点的场强就变为$\frac{E}{2}$ | |
| C. | 若在该点放一个电量为-2q的检验电荷,该点场强大小仍为E,但场强的方向变为与原来相反的方向 | |
| D. | 若在该点放一个电量为-$\frac{q}{2}$的检验电荷,则该点的场强大小仍为E,方向与原来的方向相同 |
