题目内容
2. 如图所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连.弹簧处于自然长度时物块位于O点(图中未标出).物块的质量为m,AB=a,物块与桌面间的动摩擦因数为μ.现用水平向右的力将物块从O点拉至A点,拉力做的功为W.撤去拉力后物块由静止向左运动,经O点到达B点时速度为零.重力加速度为g.则上述过程中( )
如图所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连.弹簧处于自然长度时物块位于O点(图中未标出).物块的质量为m,AB=a,物块与桌面间的动摩擦因数为μ.现用水平向右的力将物块从O点拉至A点,拉力做的功为W.撤去拉力后物块由静止向左运动,经O点到达B点时速度为零.重力加速度为g.则上述过程中( )| A. | 物块在A点时,弹簧的弹性势能等于W-$\frac{μmga}{2}$ | |
| B. | 物块在B点时,弹簧的弹性势能小于W-$\frac{3μmga}{2}$ | |
| C. | 物块经O点时,物块的动能等于W-μmga | |
| D. | 物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能 |
分析 到达B点时速度为0,但加速度不一定是零,即不一定合力为0,这是此题的不确定处.弹簧作阻尼振动,如果接触面摩擦系数μ很小,则动能为最大时弹簧伸长量较小(此时弹力等于摩擦力μmg),而弹簧振幅变化将很小,B点弹簧伸长大于动能最大点;如果μ较大,则动能最大时,弹簧伸长量较大,(因弹力等于摩擦力,μ较大,摩擦力也较大,同一个弹簧,则需要较大伸长量,弹力才可能与摩擦力平衡),而此时振幅变化很大,即振幅将变小,则物块将可能在离O点很近处,就处于静止(速度为0,加速度也为0),此时B点伸长量可能小于动能最大时伸长量.至于物块在A点或B点时弹簧的弹性势能,由功能关系和动能定理分析讨论即可.
解答 解:A、如果没有摩擦力,则O点应该在AB中间,由于有摩擦力,物体从A到B过程中机械能损失,故无法到达没有摩擦力情况下的B点,也即O点靠近B点.故OA>$\frac{a}{2}$,此过程物体克服摩擦力做功大于$\frac{1}{2}μmga$,根据能量守恒得,物块在A点时,弹簧的弹性势能小于W-$\frac{1}{2}μmga$.故A错误.
B、由A分析得物块从开始运动到最终停在B点,路程大于a+$\frac{a}{2}$,故整个过程物体克服阻力做功大于$\frac{3}{2}μmga$,故物块在B点时,弹簧的弹性势能小于$W-\frac{3}{2}μmga$.故B正确.
C、从O点开始到再次到达O点,物体路程大于a,故由动能定理得,物块的动能小于W-μmga.故C错误.
D、如果没有摩擦力,动能最大时,弹簧形变量为零,弹性势能为零,而水平面间有摩擦力,知动能最大时,弹力与摩擦力平衡,则弹性势能不为零;同时由于受到最大时的弹簧的形变量与B点时弹簧的形变量之间的关系未知,所以不能判断出物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能,故D错误.
故选:B.
点评 利用反证法得到而得到O点并非AB连线的中点是很巧妙的,此外要求同学对功能关系和动能定理理解透彻.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面(设为零势能面),现将质量相同的两个小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )
如图所示,两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面(设为零势能面),现将质量相同的两个小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )| A. | 两球的速度大小相等 | B. | 两球的速度大小不相等 | ||
| C. | 两球的机械能不相等 | D. | 两球对碗底的压力大小相等 |
 如图所示,两个完全相同的小球a、b,a从光滑斜面顶端从静止开始下滑,同时b从同一高度自由下落,两球最后都到达同一水平面.比较它们的上述运动过程,下列判断正确的是( )
如图所示,两个完全相同的小球a、b,a从光滑斜面顶端从静止开始下滑,同时b从同一高度自由下落,两球最后都到达同一水平面.比较它们的上述运动过程,下列判断正确的是( )| A. | a、b两球一定同时到达水平面 | |
| B. | 重力对a、b两球的冲量相同 | |
| C. | 重力对a、b两球做的功相同 | |
| D. | 重力对a、b两球做功的平均功率相同 |
| A. | tanθ | B. | cotθ | C. | cot2θ | D. | tan2θ |
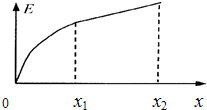 在某集装箱码头上,一架起重机将放在地面上的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中0~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )
在某集装箱码头上,一架起重机将放在地面上的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中0~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )| A. | 0~x1过程中钢绳的拉力逐渐增大 | |
| B. | 0~x1过程中箱子的动能一直增加 | |
| C. | x1~x2过程中钢绳的拉力一直不变 | |
| D. | x1~x2过程中起重机的输出功率一直增大 |
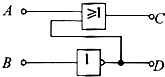 在如图所示的逻辑电路中,当A端输入电信号“1”、B端输入电信号“1”时,则在C端输出的电信号为1,D端输出的电信号为0.(填“1”或“0”)
在如图所示的逻辑电路中,当A端输入电信号“1”、B端输入电信号“1”时,则在C端输出的电信号为1,D端输出的电信号为0.(填“1”或“0”) 如图所示,是某弹簧振子做简谐运动的振动图象.在t=0s到t=0.8s时间段内,和t=0.3s时刻速度大小和方向都相同的时刻是t=0.5s;和t=0.3s时刻加速度大小和方向都相同的时刻是t=0.1s.从t=0s到t=1.2s期间振子运动通过的总路程是x=1.24cm.
如图所示,是某弹簧振子做简谐运动的振动图象.在t=0s到t=0.8s时间段内,和t=0.3s时刻速度大小和方向都相同的时刻是t=0.5s;和t=0.3s时刻加速度大小和方向都相同的时刻是t=0.1s.从t=0s到t=1.2s期间振子运动通过的总路程是x=1.24cm.