题目内容
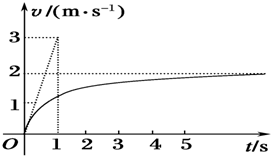
在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ、风帆受到向后的空气阻力与滑块下滑的速度v大小成正比,即f=kv.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.
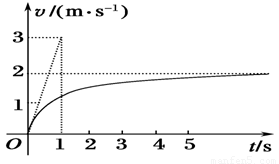
(1)由图象求滑块下滑的最大加速度和最大速度的大小;
(2)若m=2 kg,θ=37°,g=10m/s2,求出μ和k的值.(sin37°=0.6,cos37°=0.8)
【答案】
(1)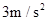 2m/s (2) μ=0.375 k=3 N·s/m
2m/s (2) μ=0.375 k=3 N·s/m
【解析】
试题分析:速度图线的切线的斜率表示加速度的大小,开始时切线斜率最大,加速度最大,速度图线逐渐接近某一数值,这一数值就是最大速度。
(1)由图象知: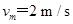
t=0时,加速度a最大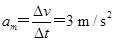 .
.
(2)根据牛顿第二定律得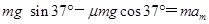
解得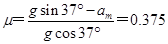
达最大速度后,滑块做匀速直线运动,有:
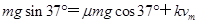
解得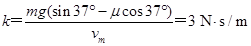 .
.
考点:牛顿第二定律应用
点评:根据图像解题一要看清坐标轴的物理意义,知道斜率、截距、渐近线等的意义。

练习册系列答案
相关题目
 (2006?徐州一模)在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ、风帆受到向后的空气阻力与滑块下滑的速度大小成正比,即f=kv.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.
(2006?徐州一模)在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ、风帆受到向后的空气阻力与滑块下滑的速度大小成正比,即f=kv.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.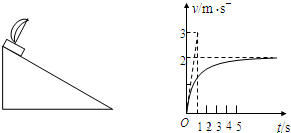 在倾斜角为θ=37°的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m=2kg,滑块与斜面间的动摩擦因数为μ,风帆受到的向后的空气阻力与滑块下滑的速度大小成正比,即f=kv.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.(sin37°=0.6,cos37°=0.8,g=10m/s2)
在倾斜角为θ=37°的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m=2kg,滑块与斜面间的动摩擦因数为μ,风帆受到的向后的空气阻力与滑块下滑的速度大小成正比,即f=kv.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.(sin37°=0.6,cos37°=0.8,g=10m/s2)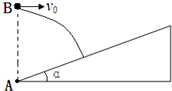 如图所示,一足够长斜面的倾斜角为α=45°.现在斜面底端A的正上方某一位置B处将一小球以速度v0水平抛出,使小球做平抛运动,小球最终垂直打在斜面上,重力加速度为g.求A、B的高度差h.
如图所示,一足够长斜面的倾斜角为α=45°.现在斜面底端A的正上方某一位置B处将一小球以速度v0水平抛出,使小球做平抛运动,小球最终垂直打在斜面上,重力加速度为g.求A、B的高度差h.
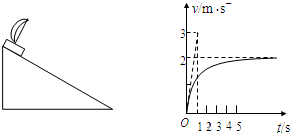 在倾斜角为θ=37°的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m=2kg,滑块与斜面间的动摩擦因数为μ,风帆受到的向后的空气阻力与滑块下滑的速度大小成正比,即f=kv.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.(sin37°=0.6,cos37°=0.8,g=10m/s2)
在倾斜角为θ=37°的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m=2kg,滑块与斜面间的动摩擦因数为μ,风帆受到的向后的空气阻力与滑块下滑的速度大小成正比,即f=kv.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.(sin37°=0.6,cos37°=0.8,g=10m/s2)