题目内容
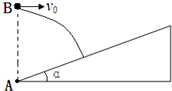如图所示，一足够长斜面的倾斜角为α=45°．现在斜面底端A的正上方某一位置B处将一小球以速度v0水平抛出，使小球做平抛运动，小球最终垂直打在斜面上，重力加速度为g．求A、B的高度差h．分析：小球垂直撞在斜面上，速度与斜面垂直，将该速度进行分解，根据水平分速度和角度关系求出竖直分速度，再根据vy=gt求出小球在空中的飞行时间．根据h=
gt2及几何关系求出A、B的高度差h．
| 1 |
| 2 |
解答：解：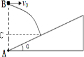
小球垂直打在斜面上，知速度与斜面垂直，根据平行四边形定则有：vy=v0tan45°=v0
根据vy=gt，解得t=
则水平位移x=v0t=
竖直位移y=
gt2=
．
则A、B的高度差h=y+xtan45°=
．
答：A、B的高度差为
．
小球垂直打在斜面上，知速度与斜面垂直，根据平行四边形定则有：vy=v0tan45°=v0根据vy=gt，解得t=
| v0 |
| g |
则水平位移x=v0t=
| v02 |
| g |
竖直位移y=
| 1 |
| 2 |
| v02 |
| 2g |
则A、B的高度差h=y+xtan45°=
| 3v02 |
| 2g |
答：A、B的高度差为
3
| ||
| 2g |
点评：该题是平抛运动基本规律的应用，主要抓住撞到斜面上时水平速度和竖直方向速度的关系以及位移的关系解题，难度适中．
练习册系列答案
新思维寒假作业系列答案
相关题目
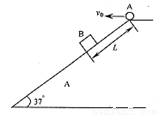
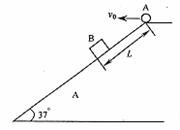
如图所示，一足够长的固定斜面与水平方向的夹角为θ=37°，物体B与斜面间的动摩擦因数为μ=0.5．将物体A以初速度v0从斜面顶端水平抛出的同时，物体B在斜面上距顶端L=16.5m处由静止释放，经历时间t，物体A第一次落到斜面上时，恰与物体B相碰，已知sin37°=0.6，cos37°=0.8，g=10m/s2，不计空气阻力，两物体都可视为质点．求：v0和t的大小．
