题目内容
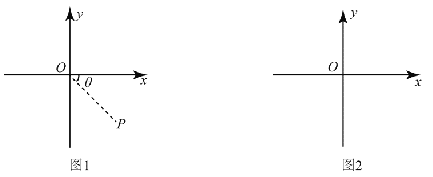
【题目】在现代科学实验和技术设备中,可以通过施加适当的电场、磁场来改变或控制带电粒子的运动。现用电场或磁场来控制质量为m 、电荷量为q 的正电荷的运动。如图1 所示,在xOy 平面内有一点P,OP与x轴夹角θ=45°,且OP=l,不计电荷的重力。
(1)若该电荷以速度v0从O 点沿x 轴正方向射出,为使电荷能够经过P 点,a.若在整个空间只加一平行于y 轴方向的匀强电场,求电场强度E 的大小和方向;
b.若在整个空间只加一垂直于xOy平面的匀强磁场,求磁感应强度B 的大小和方向。
(2)若整个空间同时存在(1)中的电场和磁场,某时刻将该电荷从O 点由静止释放,该电荷能否再次回到O 点?请你在图2 中大致画出电荷的运动轨迹。
【答案】(1)![]() 方向垂直xOy 平面向外;
方向垂直xOy 平面向外;
(2)电荷不能回到O 点,轨迹见解析。
【解析】试题分析:(1)a.电荷在电场中做类平抛运动,电荷要运动到P 点,则电场方向为y 轴负向由图可知水平方向位移为![]() 联立:
联立:
 ,
,
b.空间中存在磁场,则正电荷在其中仅受洛伦兹力做圆周运动,由初速度方向及落点,则正电荷在磁场中运动轨迹如图所示。
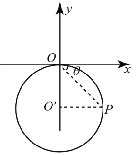
由洛伦兹力提供向心力得:![]() ,方向垂直xOy 平面向外。
,方向垂直xOy 平面向外。
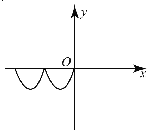
(2)空间存在沿y 轴负方向的匀强电场E 和垂直xOy 平面向外的匀强磁场B 。物体初始处于静止状态,可以看作是水平向左的速度v 与水平向右的速度v 的合成。其中令![]() 。这样,电荷之后的运动可以看作是水平向左的速度v 引起的运动,与水平向右的速度v 引起的运动的合成。对于水平向左的速度v ,对应的洛伦兹力 f = qvB =qE ,方向竖直向上,刚好与电场力平衡,因此该分运动是向右的匀速直线运动。对于水平向左的初速度v ,受到洛伦兹力,产生的是顺时针方向的匀速圆周运动。因此,电荷的运动是向右的匀速直线运动和顺时针方向的匀速圆周运动的合成,运动轨迹大致如图(此轨迹可以证明是一条摆线)。电荷不能回到O 点。
。这样,电荷之后的运动可以看作是水平向左的速度v 引起的运动,与水平向右的速度v 引起的运动的合成。对于水平向左的速度v ,对应的洛伦兹力 f = qvB =qE ,方向竖直向上,刚好与电场力平衡,因此该分运动是向右的匀速直线运动。对于水平向左的初速度v ,受到洛伦兹力,产生的是顺时针方向的匀速圆周运动。因此,电荷的运动是向右的匀速直线运动和顺时针方向的匀速圆周运动的合成,运动轨迹大致如图(此轨迹可以证明是一条摆线)。电荷不能回到O 点。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案