Question

【题目】如图所示，甲、乙传送带倾斜于水平地面放置，并以相同的恒定速率v逆时针运动，两传送带粗糙程度不同，但长度、倾角均相同．将一小物体分别从两传送带顶端的A点无初速度释放，甲传送带上物体到达底端B点时恰好达到速度v；乙传送带上物体到达传送带中部的C点时恰好达到速度v，接着以速度v运动到底端B点．则物体从A运动到B的过程中 (　　)

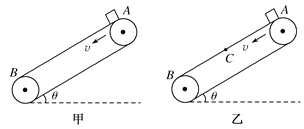
A. 物体在甲传送带上运动的时间比乙大

B. 物体与甲传送带之间的动摩擦因数比乙大

C. 两传送带对物体做功相等

D. 两传送带因与物体摩擦产生的热量相等

Answer 1

【答案】AC

【解析】A、根据两个物体的总位移相等，图象的“面积”表示位移，作出两个物体的图象，可知，故A正确；

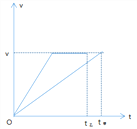
B、图象的斜率表示加速度，由图知，甲匀加速运动的加速度小于乙匀加速运动的加速度，由牛顿第二定律得：，得
则知小时，a小，因此物体与甲传送带之间的动摩擦因数比乙小，故B错误；
C、根据动能定理得： ，则得传送带对物体做功，h、v、m都相等，则W相等，故C正确；
D、设传送带长为L，甲中：物体运动时间为：，物体与传送带间的相对位移大小为：，物体的加速度为：
由牛顿第二定律得：，得：

产生的热量为：

乙中：物体运动时间为：，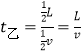
物体与传送带间的相对位移大小为：

物体的加速度为：
由牛顿第二定律得：，得：

产生的热量为：，则知乙与物体摩擦产生的热量较多，故D错误。