题目内容
长L=0.5 m、质量可忽略的杆,其一端固定于O点,另一端连有质量m=2 kg的小球,它绕O点在竖直平面内做圆周运动.当通过最高点时,如图所示,求下列情况下,杆受到的力(计算出大小,并说明是拉力还是压力,g取10 m/s2):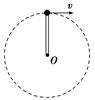
(1)当v=1 m/s时,杆受到的力多大,是什么力?
(2)当v=4 m/s时,杆受到的力多大,是什么力?
(1)16N,方向竖直向下;(2)44N,方向竖直向上。
解析试题分析:(1)当v=1 m/s时,小球所需向心力F1= =
=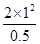 N=4 N<mg,
N=4 N<mg,
由于所需向心力小于重力,则杆对球为支持力,受力如图.
由牛顿第二定律可得,小球满足mg-N= ,则N=mg-
,则N=mg- =16 N
=16 N
由牛顿第三定律可知,杆受到压力N′=16 N,方向竖直向下.
(2)当v=4 m/s时,小球所需向心力F2= =64 N>mg
=64 N>mg
显然重力不能提供足够的向心力,则杆对球有一拉力,受力如图所示.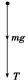
小球满足mg+T= ,即T=
,即T= -mg=44 N
-mg=44 N
由牛顿第三定律可知,小球对杆有一拉力,大小T′=44 N,方向竖直向上.
考点:向心力大小的计算,受力分析。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
在某次游戏中,两位同学对面站立、手掌相对并用力推对方,关于这两个人的推力下列理解正确的是( )
| A.力气大的一方给对方的推力大于对方给他的推力 |
| B.由于作用力和反作用力总是大小相等的,所以谁也推不动对方 |
| C.两人的推力同时出现,同时增大,同时消失 |
| D.两人的推力大小相等,方向相反,作用在同一条直线上,因此是一对平衡力 |
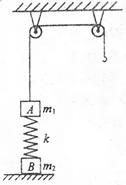
 圆弧光滑轨道,底端与传送带相切。传送带长也为R。传送带右端接光滑的水平面,水平面上静止放置一质量为3m的小物块B。一质量为m的小物块A从圆弧轨道顶端由静止释放,经过传送带后与B发生碰撞,碰后A以碰前速率的一半反弹。A与B碰撞后马上撤去圆弧轨道。已知物块A与传送带的动摩擦因数为μ=0.5,取重力加速度为g,传送带逆时针运动的速度的取值范围为
圆弧光滑轨道,底端与传送带相切。传送带长也为R。传送带右端接光滑的水平面,水平面上静止放置一质量为3m的小物块B。一质量为m的小物块A从圆弧轨道顶端由静止释放,经过传送带后与B发生碰撞,碰后A以碰前速率的一半反弹。A与B碰撞后马上撤去圆弧轨道。已知物块A与传送带的动摩擦因数为μ=0.5,取重力加速度为g,传送带逆时针运动的速度的取值范围为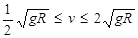 .求:
.求: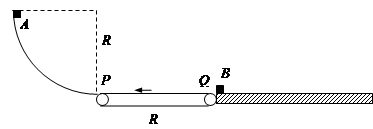
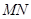 、
、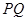 相距为
相距为 ,三根质量均为
,三根质量均为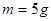 的导体棒
的导体棒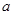 、
、 、
、 相距一定距离垂直放在导轨上且与导轨间动摩擦因数均为
相距一定距离垂直放在导轨上且与导轨间动摩擦因数均为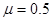 ,导体棒
,导体棒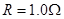 ,导体棒
,导体棒 。有磁感应强度为
。有磁感应强度为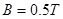 的范围足够大的匀强磁场垂直于导轨平面方向向上。现用一平行于导轨水平向右的足够大的拉力F作用在导体棒
的范围足够大的匀强磁场垂直于导轨平面方向向上。现用一平行于导轨水平向右的足够大的拉力F作用在导体棒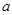 上,使之由静止开始向右做加速运动,导体棒始终与导轨垂直且接触良好,设最大静摩擦力等于滑动摩擦力,忽略导体棒间的相互作用,求:
上,使之由静止开始向右做加速运动,导体棒始终与导轨垂直且接触良好,设最大静摩擦力等于滑动摩擦力,忽略导体棒间的相互作用,求: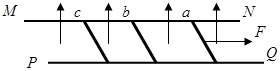
 刚开始运动时,导体棒
刚开始运动时,导体棒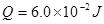 ,撤去拉力F后导体棒
,撤去拉力F后导体棒