题目内容
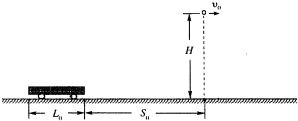
 如图所示,一辆平板小车静止在水平地面上,小车的右端放置一物块(可视为质点).已知小车的质量M=4.0kg,长度l=1.0m,其上表面离地面的高度h=0.80m.物块的质量m=1.0kg,它与平板小车间的动摩擦因数μ=0.20.若用水平向右的恒定拉力F=18N拉小车,经过一段时间后,物块从小车左端滑出.不计小车与地面间的摩擦.取g=10m/s2,求:
如图所示,一辆平板小车静止在水平地面上,小车的右端放置一物块(可视为质点).已知小车的质量M=4.0kg,长度l=1.0m,其上表面离地面的高度h=0.80m.物块的质量m=1.0kg,它与平板小车间的动摩擦因数μ=0.20.若用水平向右的恒定拉力F=18N拉小车,经过一段时间后,物块从小车左端滑出.不计小车与地面间的摩擦.取g=10m/s2,求:(1)物块在小车上滑动过程中,拉力F所做的功;
(2)物块落地时的动能;
(3)假设只改变M,m,μ,F中一个物理量的大小,使得物块在小车上运动时的速度总是平板小车的
| 2 | 3 |
分析:(1)设物块运动的加速度为a1,小车运动的加速度为a2,物块从开始滑动到从小车左端滑出的时间为t,根据牛顿第二定律及运动学基本公式结合几何关系即可求解滑块从小车左端滑出时小车的位移,根据W=Fx即可求解拉动小车过程中拉力F所做的功;
(2)物块滑出后做平抛运动,根据机械能守恒列式即可求解物块落地时的动能;
(3)小车和物体均是由静止开始做匀加速直线运动,要使物块在小车上运动时的速度总是平板小车的
倍,就必须使物体的加速度是小车加速度的
;受力分析后根据牛顿第二定律列式求解即可.
(2)物块滑出后做平抛运动,根据机械能守恒列式即可求解物块落地时的动能;
(3)小车和物体均是由静止开始做匀加速直线运动,要使物块在小车上运动时的速度总是平板小车的
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:(1)设物块运动的加速度为a1,小车运动的加速度为a2,物块从开始滑动到从小车左端滑出的时间为t.
物块所受摩擦力f=μmg,
根据牛顿第二定律f=ma1,物块的位移x1=
a1t2
小车所受摩擦力f′=f=μmg,
根据牛顿第二定律F-f′=Ma2,小车的位移x2=
a2t2
解得物块运动的加速度为a1=2 m/s2,
小车运动的加速度a2=4m/s2
由如图1所示的几何关系可知 x2-x1=l
解得滑块在t=1s末从小车左端滑出,
小车的位移x2=
a2t2=2m,
拉力F所做的功W=Fx2=36J
(2)此时物块的速度大小v1=a1t=2m/s
物块滑出后做平抛运动,
机械能守恒,
mv12+mgh=E 1′
物块落地时的动能为E 1′=10J
(3)小车和物体均是由静止开始做匀加速直线运动,要使物块在小车上运动时的速度总是平板小车的
倍,就必须使物体的加速度是小车加速度的
,即:
a1=
a2
物体受重力、支持力和向前的滑动摩擦力,根据牛顿第二定律,有:
μmg=ma1
小车受重力、支持力、压力、物体对其向后的滑动摩擦力,根据牛顿第二定律,有:
F-μmg=Ma2
联立以上三式得到:μg=
(
-
)
若改变F,则F=14N;
答:(1)拉动小车过程中拉力F所做的功为36J;
(2)物块落地时的动能10J;
(3)只改变F到14N,可使得物块在小车上运动时的速度总是平板小车的
倍.
物块所受摩擦力f=μmg,
根据牛顿第二定律f=ma1,物块的位移x1=
| 1 |
| 2 |
小车所受摩擦力f′=f=μmg,
根据牛顿第二定律F-f′=Ma2,小车的位移x2=
| 1 |
| 2 |
解得物块运动的加速度为a1=2 m/s2,
小车运动的加速度a2=4m/s2
由如图1所示的几何关系可知 x2-x1=l
解得滑块在t=1s末从小车左端滑出,
小车的位移x2=
| 1 |
| 2 |
拉力F所做的功W=Fx2=36J
(2)此时物块的速度大小v1=a1t=2m/s
物块滑出后做平抛运动,
机械能守恒,
| 1 |
| 2 |
物块落地时的动能为E 1′=10J
(3)小车和物体均是由静止开始做匀加速直线运动,要使物块在小车上运动时的速度总是平板小车的
| 2 |
| 3 |
| 2 |
| 3 |
a1=
| 2 |
| 3 |
物体受重力、支持力和向前的滑动摩擦力,根据牛顿第二定律,有:
μmg=ma1
小车受重力、支持力、压力、物体对其向后的滑动摩擦力,根据牛顿第二定律,有:
F-μmg=Ma2
联立以上三式得到:μg=
| 2 |
| 3 |
| F |
| M |
| μmg |
| M |
若改变F,则F=14N;
答:(1)拉动小车过程中拉力F所做的功为36J;
(2)物块落地时的动能10J;
(3)只改变F到14N,可使得物块在小车上运动时的速度总是平板小车的
| 2 |
| 3 |
点评:本题主要考查了牛顿第二定律、运动学基本公式、平抛运动的基本规律的直接应用,要求同学们能正确分析物体和小车的运动情况,并能结合几何关系求解,难度适中.

练习册系列答案
相关题目
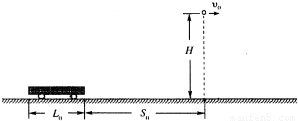
 如图所示,一辆平板小车,车长为L0,沿着光滑的水平地面由静止开始,以加速度a向右做匀加速运动,与此同时,在小车的正前方S0处的正上方H高处,有一个可视为质点的小球以初速度v0水平向右抛出,重力加速度为g,不计小车高度,问加速度a满足什么条件小球可以落到小车上?
如图所示,一辆平板小车,车长为L0,沿着光滑的水平地面由静止开始,以加速度a向右做匀加速运动,与此同时,在小车的正前方S0处的正上方H高处,有一个可视为质点的小球以初速度v0水平向右抛出,重力加速度为g,不计小车高度,问加速度a满足什么条件小球可以落到小车上?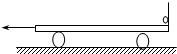 如图所示,一辆上表面光滑的平板小车长2m,上表面距离地面高0.8m,车上右侧有一挡板,紧靠挡板有一可视为质点的小球.开始时,小车与小球一起在水平面上向左以速度5m/s做匀速直线运动.某时刻小车开始刹车,加速度大小为4m/s2.经过一段时间,小球从小车的左端滑出小车并落到地面上.g取10m/s2.试求:
如图所示,一辆上表面光滑的平板小车长2m,上表面距离地面高0.8m,车上右侧有一挡板,紧靠挡板有一可视为质点的小球.开始时,小车与小球一起在水平面上向左以速度5m/s做匀速直线运动.某时刻小车开始刹车,加速度大小为4m/s2.经过一段时间,小球从小车的左端滑出小车并落到地面上.g取10m/s2.试求: