题目内容
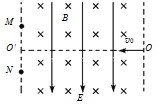
【题目】如图所示,空间存在一匀强电场,其方向与水平方向夹角为 30°,A、B连线与电场线垂直,一质量为 m,电荷量为 q的带正电小球以初速度 v0 从 A点水平向右抛出,经过时间 t小球最终落在 C 点,速度大小仍为v0,且 AB=BC,则下列说法中正确的是

A. 电场强度方向沿电场线斜向上 B. 电场强度大小为E=![]()
C. 此过程小球增加的电势能等于![]() D. 小球在运动过程中下落的高度为
D. 小球在运动过程中下落的高度为![]()
【答案】C
【解析】小球在下落过程中初末动能不变,由动能定理可知,mgABsin60°-EqBCsin60°=0,解得:E=![]() ;由题意可知,小球在下落过程中初末动能不变,根据动能定理,合力做功为0,而重力做正功,则电场力做负功,而小球带正电,故电场线应斜向下;故AB错误; 将电场力分解为沿水平方向和竖直方向,
;由题意可知,小球在下落过程中初末动能不变,根据动能定理,合力做功为0,而重力做正功,则电场力做负功,而小球带正电,故电场线应斜向下;故AB错误; 将电场力分解为沿水平方向和竖直方向,


则有竖直分量中产生的电场力F=E′q=mgcos60°=![]() mg;则物体在竖直方向上的合力F合=
mg;则物体在竖直方向上的合力F合=![]() mg;则由牛顿第二定律可知,竖直方向上的分加速度ay=
mg;则由牛顿第二定律可知,竖直方向上的分加速度ay=![]() g;则下落高度
g;则下落高度![]() ;故D错误;此过程中电场力做负功,电势能增加,由几何关系可知,小球在沿电场线的方向上的位移
;故D错误;此过程中电场力做负功,电势能增加,由几何关系可知,小球在沿电场线的方向上的位移![]() ;则电势能的增加量
;则电势能的增加量![]() ;故C正确;故选C.
;故C正确;故选C.

练习册系列答案
相关题目