题目内容
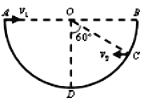
【题目】如图所示，M、N、P为很长的平行边界面，M、N与M、P间距分别为l1、l2，其间分别有磁感应强度为B1和B2的匀强磁场区，Ⅰ和Ⅱ磁场方向垂直纸面向里，B1≠B2，有一带正电粒子的电量为q，质量为m，以某一初速度垂直边界N及磁场方向射入MN间的磁场区域．不计粒子的重力．求：
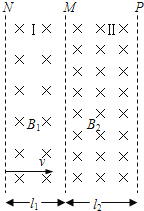
（1）要使粒子能穿过Ⅰ磁场进入Ⅱ磁场，粒子的初速度v0至少应为多少？
（2）若粒子进入磁场的初速度v1=
，则粒子第一次穿过Ⅰ磁场的时间t1是多少？
（3）粒子初速度v为多少时，才可恰好穿过两个磁场区域．
【答案】（1）
；
（2）
；
（3）
．
【解析】解：（1）粒子的初速度为v0时恰好能进入Ⅱ磁场，则进入Ⅱ磁场时速度恰好沿M边界，所以半径为r=l1，则
B1qv0=
解得：
（2）粒子在磁场中运动，
B1q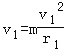
解得：r1=2l1
粒子在Ⅰ磁场中作匀速圆周对应的圆心角为α，
sinα=
=
所以：α=
所以第一次穿过Ⅰ磁场的时间为：
=
（3）设粒子速度为v时，粒子在B2磁场中的轨迹恰好与P边界相切，轨迹如图所示，
由Bqv=
可得：
，
sinθ=
=
粒子在B2中运动有：R2﹣R2sinθ=l2
解得：v=
答：（1）要使粒子能穿过Ⅰ磁场进入Ⅱ磁场，粒子的初速度v0至少应为；
（2）若粒子进入磁场的初速度
，则粒子第一次穿过Ⅰ磁场的时间t1是；
（3）粒子初速度v为时，才可恰好穿过两个磁场区域．
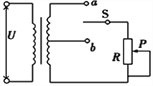
愉快的寒假南京出版社系列答案
【题目】某实验小组测定水果电池的电动势和内电阻，所用的器材有：
水果电池E：电动势约为1V； 电流表A：量程10mA，内阻约为几欧；
电压表V：量程1V，内阻RV=3kΩ； 滑动变阻器Rp：最大阻值200Ω；
电阻箱R：最大阻值9999Ω； 开关S，导线若干。
（1）该实验小组设计了如图1所示的电路，实验中无论怎样移动滑动变阻器的滑片，发现电流表的示数及变化均很小，且电压表的示数变化很小，分析其原因是_____________________。
（2）该实验小组经过分析设计了如图所示的电路，实验步骤如下：
第一步：闭合开关S，多次调节电阻箱，记下电压表的示数U和电阻箱相应的阻值R，并计算出对应的
与
的值。
第二步：以为纵坐标，为横坐标，作出－图线（用直线拟合）。
第三步：求出直线的斜率k和在纵轴上的截距b。
请回答下列问题：
（3）实验得到的部分数据如下表所示，其中当电阻箱的电阻R= 2000Ω时电压表的示数如图所示。读出数据，完成下表。答：①________________，②________________________。
R/Ω | 9000 | 6000 | 5000 | 4000 | 3000 | 2000 |
R-1/10－4Ω-1 | 1.11 | 1.67 | 2.00 | 2.50 | 3.33 | 5.00 |
U/V | 0.53 | 0.50 | 0.48 | 0.46 | 0.43 | ① |
U-1/V-1 | 1.9 | 2.0 | 2.1 | 2.2 | 2.3 | ② |
（4）若根据－图线求得直线的斜率k=2.0×103Ω/V，截距
，则该水果电池的电动势E=_______________V，内阻r=_________________________Ω。
