题目内容
1. 如图所示,质量mB=2kg的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一质量mA=2kg的物块A,一颗质量m0=0.01kg的子弹v0=600m/s的水平初速度瞬间射穿A后,速度变为v1=200m/s.由于A与B间摩擦力作用使A与B最终到达相对静止.则整个过程中A、B组成的系统因摩擦产生热量为多少?
如图所示,质量mB=2kg的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一质量mA=2kg的物块A,一颗质量m0=0.01kg的子弹v0=600m/s的水平初速度瞬间射穿A后,速度变为v1=200m/s.由于A与B间摩擦力作用使A与B最终到达相对静止.则整个过程中A、B组成的系统因摩擦产生热量为多少?
分析 子弹射穿物块A的过程、A与B相互作用过程系统定律守恒,应用动量守恒定律求出物体的速度,然后应用能量守恒定律可以求出产生的热量.
解答 解:对于子弹、物块A相互作用过程系统动量守恒,以子弹的初速度方向为正方向,
由动量守恒定律得:m0v0=m0v1+mAvA,代入数据解得:vA=2m/s,
对于A、B相互作用过程中,以A的初速度方向为正方向,
由动量守恒定律得:mAvA=(mA+mB)v,代入数据解得:v=$\frac{2×2}{2+2}$=1m/s,
A、B系统因摩擦产生的热量等于A、B系统损失的动能,
由能量守恒定律得:△E=$\frac{1}{2}$mAvA2-$\frac{1}{2}$(mA+mB)v2,
代入数据解得:△E=2J;
答:整个过程中A、B组成的系统因摩擦产生热量为2J.
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程,应用动量守恒定律与能量守恒定律即可解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.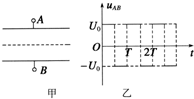 如图甲所示,一对长为L的金属板,平行正对放置,质量为m的电子从平行板左侧以速度v0沿两板的中线不断进入平行板之间.两板间所加交变电压uAB如图乙所示,交变电压的周期T=$\frac{L}{2{v}_{0}}$,已知所有电子都能穿过平行板,不考虑电子的重力和电子间的相互作用,则( )
如图甲所示,一对长为L的金属板,平行正对放置,质量为m的电子从平行板左侧以速度v0沿两板的中线不断进入平行板之间.两板间所加交变电压uAB如图乙所示,交变电压的周期T=$\frac{L}{2{v}_{0}}$,已知所有电子都能穿过平行板,不考虑电子的重力和电子间的相互作用,则( )
 如图甲所示,一对长为L的金属板,平行正对放置,质量为m的电子从平行板左侧以速度v0沿两板的中线不断进入平行板之间.两板间所加交变电压uAB如图乙所示,交变电压的周期T=$\frac{L}{2{v}_{0}}$,已知所有电子都能穿过平行板,不考虑电子的重力和电子间的相互作用,则( )
如图甲所示,一对长为L的金属板,平行正对放置,质量为m的电子从平行板左侧以速度v0沿两板的中线不断进入平行板之间.两板间所加交变电压uAB如图乙所示,交变电压的周期T=$\frac{L}{2{v}_{0}}$,已知所有电子都能穿过平行板,不考虑电子的重力和电子间的相互作用,则( )| A. | 所有电子都从右侧的同一点离开电场 | |
| B. | 电子离开电场时速度大小不可能等于v0 | |
| C. | t=0时刻进入电场的电子,离开电场时的动能大于$\frac{1}{2}$mv02 | |
| D. | 在t=0时刻进入电场的电子,在两板间运动时侧位移最大 |
9.下列说法正确的是( )
| A. | 汤姆孙发现电子,提出原子的核式结构模型 | |
| B. | 金属的逸出功随入射光的频率增大而增大 | |
| C. | 核力存在于原子核内所有核子之间 | |
| D. | 核子平均结合能越大的原子核越稳定 |
16.关于永动机和热力学定律的讨论,系列叙述正确的是 ( )
| A. | 第二类永动机违反能量守恒定律 | |
| B. | 热量不可能自发地从低温物体传到高温物体 | |
| C. | 对某物体做功,物体的内能必定增加 | |
| D. | 可以从单一热源吸收热量,使之完全变为功 | |
| E. | 能量耗散从能量转化角度反映出自然界中的宏观过程具有方向性 |
13. 如图所示,氢原子可在下列各能级间发生跃迁,设从n=4到n=1能级辐射的电磁波的波长为λ1,从n=4到n=2能级辐射的电磁波的波长为λ2,从n=2到n=1能级辐射的电磁波的波长为λ3,则下列关系式中正确的是( )
如图所示,氢原子可在下列各能级间发生跃迁,设从n=4到n=1能级辐射的电磁波的波长为λ1,从n=4到n=2能级辐射的电磁波的波长为λ2,从n=2到n=1能级辐射的电磁波的波长为λ3,则下列关系式中正确的是( )
 如图所示,氢原子可在下列各能级间发生跃迁,设从n=4到n=1能级辐射的电磁波的波长为λ1,从n=4到n=2能级辐射的电磁波的波长为λ2,从n=2到n=1能级辐射的电磁波的波长为λ3,则下列关系式中正确的是( )
如图所示,氢原子可在下列各能级间发生跃迁,设从n=4到n=1能级辐射的电磁波的波长为λ1,从n=4到n=2能级辐射的电磁波的波长为λ2,从n=2到n=1能级辐射的电磁波的波长为λ3,则下列关系式中正确的是( )| A. | λ1<λ3 | B. | λ3<λ2 | C. | λ3>λ2 | D. | $\frac{1}{{λ}_{3}}$=$\frac{1}{{λ}_{1}}$+$\frac{1}{{λ}_{2}}$ | ||||
| E. | $\frac{1}{{λ}_{3}}$=$\frac{1}{{λ}_{1}}$-$\frac{1}{{λ}_{2}}$ |
10.某河流宽420m,船在静水中的航速为4m/s,水流速度是3m/s,则船渡过该河流的最短时间( )
| A. | 140 s | B. | 105 s | C. | 84 s | D. | 60$\sqrt{7}$s |
11. 如图所示,R0为热敏电阻(温度降低电阻增大),R1为定值电阻,R是滑动变阻器,开关S闭合,C为平行板电容器,C中央有一带电液滴刚好静止,下列各项单独操作中能使带电液滴向上运动的是( )
如图所示,R0为热敏电阻(温度降低电阻增大),R1为定值电阻,R是滑动变阻器,开关S闭合,C为平行板电容器,C中央有一带电液滴刚好静止,下列各项单独操作中能使带电液滴向上运动的是( )
 如图所示,R0为热敏电阻(温度降低电阻增大),R1为定值电阻,R是滑动变阻器,开关S闭合,C为平行板电容器,C中央有一带电液滴刚好静止,下列各项单独操作中能使带电液滴向上运动的是( )
如图所示,R0为热敏电阻(温度降低电阻增大),R1为定值电阻,R是滑动变阻器,开关S闭合,C为平行板电容器,C中央有一带电液滴刚好静止,下列各项单独操作中能使带电液滴向上运动的是( )| A. | 将R0加热 | B. | R的滑动头P向上移动 | ||
| C. | C的上极板向上移动 | D. | 开关S断开 |
 一位质量m=50kg的滑雪运动员(包括滑雪板)从高度h=30m的斜坡自由滑下(初速度为零).斜坡的倾角θ=37°,滑雪板与雪面滑动摩擦因素μ=0.1.(不计空气阻力)则运动员(包括滑雪板)滑至坡底的过程中(g取10m/s2,sin37°=0.6,cos37°=0.8)
一位质量m=50kg的滑雪运动员(包括滑雪板)从高度h=30m的斜坡自由滑下(初速度为零).斜坡的倾角θ=37°,滑雪板与雪面滑动摩擦因素μ=0.1.(不计空气阻力)则运动员(包括滑雪板)滑至坡底的过程中(g取10m/s2,sin37°=0.6,cos37°=0.8)