题目内容
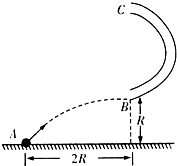 在水平地面A处以初速度v0抛出一个小球,恰好水平进入光滑的半圆轨道的最低点B,已知半圆轨道半径R=0.2m,B点离地面的高度也为R,A点到B点的水平距离为2R,求:
在水平地面A处以初速度v0抛出一个小球,恰好水平进入光滑的半圆轨道的最低点B,已知半圆轨道半径R=0.2m,B点离地面的高度也为R,A点到B点的水平距离为2R,求:(1)小球从A运动到B的时间;
(2)小球抛出时的初速度v0的大小;
(3)小球能否到达半圆轨道的最高点C.
分析:(1)小球做斜上抛运动,竖直方向上作竖直上抛运动,有R=
gt2,可求出时间t;
(2)小球水平方向做匀速运动,有2R=vxt,即可求得vx,运用速度的合成可求出初速度v0的大小;
(3)假设小球能到达C点,根据机械能守恒定律求出小球到达C点时的速度大小,与小球到达C点的临界速度为零进行比较,即可作出判断.
| 1 |
| 2 |
(2)小球水平方向做匀速运动,有2R=vxt,即可求得vx,运用速度的合成可求出初速度v0的大小;
(3)假设小球能到达C点,根据机械能守恒定律求出小球到达C点时的速度大小,与小球到达C点的临界速度为零进行比较,即可作出判断.
解答:解:(1)小球从A到B运动过程中,竖直方向上作竖直上抛运动,末速度为零,则有:R=
gt2
解得:t=0.2s.
(2)小球从A到B运动过程中,水平方向做匀速运动,设速度为v,则有:
2R=vxt,求得vx=2m/s
竖直方向的初速度 vy=gt=2m/s
故初速度v0=
=2
m/s
(2)假设小球能到达C点,并设到达C点的速度为v,根据机械能守恒定律得
3mgR=
m
-
mv2
解得,v2=-4,不合理,故小球不能到达半圆轨道的最高点C.
答:
(1)小球从A运动到B的时间是0.2s;
(2)小球抛出时的初速度v0的大小是2
m/s;
(3)小球不能到达半圆轨道的最高点C.
| 1 |
| 2 |
解得:t=0.2s.
(2)小球从A到B运动过程中,水平方向做匀速运动,设速度为v,则有:
2R=vxt,求得vx=2m/s
竖直方向的初速度 vy=gt=2m/s
故初速度v0=
|
| 2 |
(2)假设小球能到达C点,并设到达C点的速度为v,根据机械能守恒定律得
3mgR=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
解得,v2=-4,不合理,故小球不能到达半圆轨道的最高点C.
答:
(1)小球从A运动到B的时间是0.2s;
(2)小球抛出时的初速度v0的大小是2
| 2 |
(3)小球不能到达半圆轨道的最高点C.
点评:运用运动的合成与分解处理斜抛运动是常用的方法,小球在管中运动,到达最高点的临界速度为零.

练习册系列答案
相关题目
 如图所示,一可视为质点的质量为m、电荷量为q带负电小球,从距地面高为2h处以一定的初速水平度抛出,在离抛出点水平距离为s处,有一根管口比小球直径略大些的竖直细管,管的上端距地面高度为h.现欲使小球能无碰撞地通过管子,在管子上方的整个区域里加一个水平向右的匀强电场.关于此小球和电场下列说法正确的是( )
如图所示,一可视为质点的质量为m、电荷量为q带负电小球,从距地面高为2h处以一定的初速水平度抛出,在离抛出点水平距离为s处,有一根管口比小球直径略大些的竖直细管,管的上端距地面高度为h.现欲使小球能无碰撞地通过管子,在管子上方的整个区域里加一个水平向右的匀强电场.关于此小球和电场下列说法正确的是( )