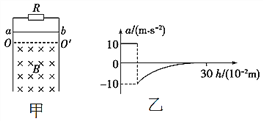��Ŀ����
����Ŀ����ͼ����ʾ���ô��ͻ�����������ͬ��Բ����ˮ��ܵ�����������װ������ܵ����ײ�ܵ��̶��ڳ�����ϲ�ܵ��ѷ��ڵײ�ܵ��ϣ���ͼ����ʾ����֪ˮ��ܵ���Ķ�Ħ��������=![]() ����������ɲ��ʱ�ļ��ٶȴ�СΪ8m/s2��ÿ���ֹܵ�������m=1500kg���������ٶ�ȡg=10m/s2����
����������ɲ��ʱ�ļ��ٶȴ�СΪ8m/s2��ÿ���ֹܵ�������m=1500kg���������ٶ�ȡg=10m/s2����
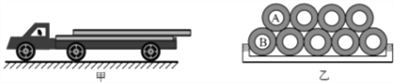
��1��������ƽֱ·��������ʻʱ����ͼ�й�A��B֮��ĵ�����С��
��2�����������ˮƽ·����������ʻ���ٶ�Ϊ43.2km/h��Ҫʹ�����ڽ���ɲ��ʱ�Ϲܵ���ײ�ϼ�ʻ�ң�����ѷ�ʱ�ϲ�ܵ���ǰ��Ӧ�����ʻ�ҵ���С������
���𰸡���1��5000![]() N��2��1.8m
N��2��1.8m
��������������������ϲ�ܵ�������������������ƽ���������������A��B֮��ĵ�����С���ȸ���ţ�ٵڶ���������ϲ�ܵ��ļ��ٶȣ�Ȼ����ݵı��ι�ʽ�ֱ��ʾ���ϲ�ܵ��ڼ�ɲ��������ͣ�º��˶����ܾ���ͻ�����ɲ�����룬����֮�Ϊ����ѷ�ʱ�ϲ�ܵ���ǰ��Ӧ�����ʻ�ҵ���С���롣
��1���ϲ�ܵ�������ڵ�����������������֧����ΪFN����ͼ��ʾ��
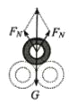
����ֱ�����У�2FNcos30��-mg=0
��ã� ![]()
��2��������֪������ɲ��ʱ�ϲ�ܵ��ܵ���������Ħ�������٣�
����ţ���˶����ɣ�2��FN=ma1
�������ݽ�ã� ![]()
��������ɲ��ʱ�ļ��ٶ�Ϊ��a2=8m/s2
�����ٶ�λ�ƹ�ʽ�ɵû�����ɲ�����룺 ![]()
�ϲ�ܵ��ڼ�ɲ��������ͣ�º��˶����ܾ��룺 ![]()
�ϲ�ܵ�����ڻ��������ľ��룺��x=x1��x2
�������ϲ��������ݽ�ã���x=1.8m

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�