题目内容
3.频率为5×1014Hz单色光通过双缝S1和S2投射到屏上,并且S1和S2振动方向相同.屏上的点P到S1与P到S2的路程差为9×10-7m,光在真空中的波长为6×10-7m,点P处形成暗条纹.分析 先根据公式c=λf求出光的波长,然后判断路程差是半波长的奇数倍还是偶数倍,若是偶数倍即波长的整数倍则出现亮条纹.
解答 解:根据光波的速度公式
c=λf
有λ=cfcf=3×1085×10143×1085×1014m=6×10-7 m
光的路程差跟光波长之比为
n=△sλ△sλ=9×10−76×10−79×10−76×10−7=4.5;
即路程差为光波长的奇数倍.因此,两束光在该点振动减弱,出现光的暗条纹.
故答案为:6×10-7,暗.
点评 本题考查双缝干涉实验中出现明暗条纹的条件,掌握光的干涉中出现明亮条纹的条件并会应用,解决本题的关键掌握双缝到光屏上P点的距离之差是波长的整数倍,则出现明条纹,路程之差是半波长的奇数倍,则出现暗条纹.

练习册系列答案
相关题目
9.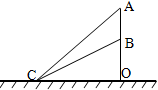 如图所示,AC和BC是两个固定的斜面,斜面的顶端在同一竖直线上.质量相同的两个物体分别自斜面AC和BC的顶端由静止开始下滑,物体与斜面间的动摩擦因数相同.从斜面AC上滑下的物体滑至底部C点时的动能为Ek1,下滑过程中克服摩擦力所做的功为W1;从斜面BC上滑下的物体滑至底部C点时的动能为Ek2,下滑过程中克服摩擦力所做的功为W2,则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端在同一竖直线上.质量相同的两个物体分别自斜面AC和BC的顶端由静止开始下滑,物体与斜面间的动摩擦因数相同.从斜面AC上滑下的物体滑至底部C点时的动能为Ek1,下滑过程中克服摩擦力所做的功为W1;从斜面BC上滑下的物体滑至底部C点时的动能为Ek2,下滑过程中克服摩擦力所做的功为W2,则( )
 如图所示,AC和BC是两个固定的斜面,斜面的顶端在同一竖直线上.质量相同的两个物体分别自斜面AC和BC的顶端由静止开始下滑,物体与斜面间的动摩擦因数相同.从斜面AC上滑下的物体滑至底部C点时的动能为Ek1,下滑过程中克服摩擦力所做的功为W1;从斜面BC上滑下的物体滑至底部C点时的动能为Ek2,下滑过程中克服摩擦力所做的功为W2,则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端在同一竖直线上.质量相同的两个物体分别自斜面AC和BC的顶端由静止开始下滑,物体与斜面间的动摩擦因数相同.从斜面AC上滑下的物体滑至底部C点时的动能为Ek1,下滑过程中克服摩擦力所做的功为W1;从斜面BC上滑下的物体滑至底部C点时的动能为Ek2,下滑过程中克服摩擦力所做的功为W2,则( )| A. | Ek1<Ek2,W1>W2 | B. | Ek1>Ek2,W1>W2 | C. | Ek1>Ek2,W1=W2 | D. | Ek1<Ek2,W1<W2 |
10. 如图所示,质量为m的小球,从桌面边缘A处以初速度V离开高为H的桌面,经B点到达地面C处.B点距地面高为h,不计空气阻力,下列判断正确的是( )
如图所示,质量为m的小球,从桌面边缘A处以初速度V离开高为H的桌面,经B点到达地面C处.B点距地面高为h,不计空气阻力,下列判断正确的是( )
 如图所示,质量为m的小球,从桌面边缘A处以初速度V离开高为H的桌面,经B点到达地面C处.B点距地面高为h,不计空气阻力,下列判断正确的是( )
如图所示,质量为m的小球,从桌面边缘A处以初速度V离开高为H的桌面,经B点到达地面C处.B点距地面高为h,不计空气阻力,下列判断正确的是( )| A. | 若取A处为参考面,小球在B点具有的机械能是 mV22mV22 | |
| B. | 若取B处为参考面,小球在A点具有的机械能是 mV22mV22+mgh | |
| C. | 若取地面为参考面,小球在C点的动能等于A处的机械能与A到C重力做功的代数和 | |
| D. | 小球从A运动到B、再从B运动到C,机械能的改变量一定相等 |
7.用打点计时器研究匀变速直线运动的实验中,造成各连续相等的时间间隔内位移之差不是一个恒量的主要原因是( )
| A. | 长度测量不准 | B. | 时间间隔不是0.02s而是0.18s | ||
| C. | 运动中摩擦力作用 | D. | 木板未调成水平 |
14.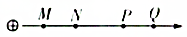 如图所示,M、N、P、Q是正点电荷电场线上四点,且MN=PQ,由此可以判断( )
如图所示,M、N、P、Q是正点电荷电场线上四点,且MN=PQ,由此可以判断( )
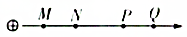 如图所示,M、N、P、Q是正点电荷电场线上四点,且MN=PQ,由此可以判断( )
如图所示,M、N、P、Q是正点电荷电场线上四点,且MN=PQ,由此可以判断( )| A. | UMN=UPQ | B. | UMN>UPQ | C. | UMN<UPQ | D. | 无法判断 |