题目内容
12.过山车的玩法很多,如图A、B就是其中的两种,将这两种过山车简化成车在外轨道和内轨道运动,假设这两种过山车做的都是圆周运动,做圆周运动的半径为R,重力加速度为g,不考虑各种摩擦阻力,则:
(1)在图A中,通过最高点时人对座位刚好没有压力,在最高点速度是多少?
(2)在图A中,在圆形轨道的最低点安装一个测力传感器,传感器的示数在多大范围时,过山车才能安全通过最高点,已知过山车和人的总质量为M
(3)在图B中,要求过山车在最高点时对轨道的压力是其重力的1倍到3倍,则最开始释放的位置距离轨道最低点高度.
分析 (1)在图A中,当过山车到圆形轨道最高点人对座位没有压力,即只受重力作用,根据重力提供向心力可知求解;
(2)在图A中,要能安全通过最高点,则在最高点:$0<v<\sqrt{gR}$,从最低点到最高点过程根据动能定理列式,在最低点,根据向心力公式列式,联立方程求解;
(3)图B中,在最高点,根据向心力公式列式,从释放位置到圆形轨道最高点过程中,根据动能定理列式,联立方向即可求解.
解答 解:(1)在图A中,当过山车到圆形轨道最高点人对座位没有压力,即只受重力作用,则有
mg=$m\frac{{v}^{2}}{R}$
解得:v=$\sqrt{gR}$
(2)在图A中,要能安全通过最高点,则在最高点:$0<v<\sqrt{gR}$
从最低点到最高点过程:
$-Mg2R=\frac{1}{2}M{v}^{2}-\frac{1}{2}M{{v}_{1}}^{2}$
在最低点:
${F}_{N}-Mg=M\frac{{{v}_{1}}^{2}}{R}$
解得:5Mg<FN≤6Mg
(3)图B中,在最高点:
${F}_{N}′+mg=m\frac{{{v}_{2}}^{2}}{R}$
解得:mg≤FN′≤3mg
从释放位置到圆形轨道最高点过程:
$mg(h-2R)=\frac{1}{2}m{{v}_{2}}^{2}-0$
解得:4R≤h≤6R
答:(1)在图A中,通过最高点时人对座位刚好没有压力,在最高点速度是$\sqrt{gR}$;
(2)在图A中,在圆形轨道的最低点安装一个测力传感器,传感器的示数在5Mg<FN≤6Mg范围时,过山车才能安全通过最高点;
(3)在图B中,要求过山车在最高点时对轨道的压力是其重力的1倍到3倍,则最开始释放的位置距离轨道最低点高度为4R≤h≤6R.
点评 本题主要考查了向心力公式以及动能定理的直接应用,解题时要分析清楚向心力的来源,要求同学们能正确分析物体的受力情况,难度适中.

 阅读快车系列答案
阅读快车系列答案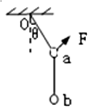 如图所示,将两个质量均为m的小球a,b用细线相连悬挂于O点,用力F拉小球a,使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=37°,则F的大小( )
如图所示,将两个质量均为m的小球a,b用细线相连悬挂于O点,用力F拉小球a,使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=37°,则F的大小( )| A. | 可能为0.5mg | B. | 可能为0.8mg | C. | 可能为mg | D. | 可能为1.5mg |
 图为卢瑟福和他的同事们做α?粒子散射实验装置的示意图,荧光屏和显微镜一起分别放在图中的A、B、C、D四个位置时,观察到的现象,下述说法中正确的是( )
图为卢瑟福和他的同事们做α?粒子散射实验装置的示意图,荧光屏和显微镜一起分别放在图中的A、B、C、D四个位置时,观察到的现象,下述说法中正确的是( )| A. | 放在A位置时,相同时间内观察到屏上的闪光次数最多 | |
| B. | 放在B 位置时,相同时间内观察到屏上的闪光次数比A位置时要少些 | |
| C. | 放在C、D 位置时,屏上观察不到闪光 | |
| D. | 放在D 位置时,屏上仍能观察到闪光,但次数极少 |
 在练习使用多用电表的实验中:
在练习使用多用电表的实验中: 如图所示,长方形木块A、B叠在一起,放在水平桌面上,A、B之间的接触面粗糙.B受到水平方向的拉力作用、但仍然保持静止.则B木块受到的力的个数是( )
如图所示,长方形木块A、B叠在一起,放在水平桌面上,A、B之间的接触面粗糙.B受到水平方向的拉力作用、但仍然保持静止.则B木块受到的力的个数是( )



 如图所示,有一原长x=0.5m、劲度系数k=100N/m的轻质弹簧穿过一光滑金属杆,弹簧一端固定在金属杆的一端点O,另一端与穿过金属杆的小球相连,小球质量m=1kg,整个装置在竖直平面内绕O点转动.取g=10m/s2,$\sqrt{13}$=3.6,$\sqrt{5}$=2.24.
如图所示,有一原长x=0.5m、劲度系数k=100N/m的轻质弹簧穿过一光滑金属杆,弹簧一端固定在金属杆的一端点O,另一端与穿过金属杆的小球相连,小球质量m=1kg,整个装置在竖直平面内绕O点转动.取g=10m/s2,$\sqrt{13}$=3.6,$\sqrt{5}$=2.24.