题目内容
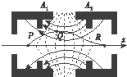
【题目】如图所示,虚线MN左侧有一场强为![]() 的匀强电场,在两条平行的虚线MN和PQ之间存在着宽为L、电场强度为
的匀强电场,在两条平行的虚线MN和PQ之间存在着宽为L、电场强度为![]() 的匀强电场,在虚线PQ右侧相距为L处有一与电场
的匀强电场,在虚线PQ右侧相距为L处有一与电场![]() 平行的屏。现将一电子(电荷量为e,质量为m,不计重力)无初速地放入电场
平行的屏。现将一电子(电荷量为e,质量为m,不计重力)无初速地放入电场![]() 中的A点,A点到MN的距离为
中的A点,A点到MN的距离为![]() ,最后电子打在右侧的屏上,AO连线与屏垂直,垂足为O,求:
,最后电子打在右侧的屏上,AO连线与屏垂直,垂足为O,求:
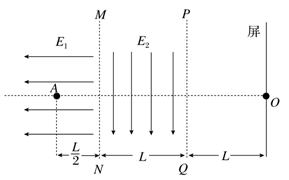
(1)电子从释放到打到屏上所用的时间t;
(2)电子刚射出电场![]() 时的速度方向与AO连线夹角
时的速度方向与AO连线夹角![]() 的正切值
的正切值![]() ;
;
(3)电子打到屏上的点![]() (图中未标出)到点O的距离x。
(图中未标出)到点O的距离x。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)电子在电场![]() 中做初速度为零的匀加速直线运动,设加速度为
中做初速度为零的匀加速直线运动,设加速度为![]() ,时间为
,时间为![]() ,
,
由牛顿第二定律得:![]() ①
①
由![]() 得:
得:![]() ②
②
电子进入电场![]() 时的速度为:
时的速度为: ![]() ③
③
进入电场![]() 到屏水平方向做匀速直线运动,时间为:
到屏水平方向做匀速直线运动,时间为:![]() ④
④
电子从释放到打到屏上所用的时间为: ![]() ⑤
⑤
联立①→⑤求解得:![]() ;
;
(2)设粒子射出电场E2时平行电场方向的速度为![]() ,由牛顿第二定律得:
,由牛顿第二定律得:
电子进入电场![]() 时的加速度为:
时的加速度为:![]() ⑥,
⑥,![]() ⑦
⑦![]() ⑧
⑧
电子刚射出电场![]() 时的速度方向与AO连线夹角的正切值为;
时的速度方向与AO连线夹角的正切值为;![]() ⑨
⑨
联立①②③⑥⑦⑧⑨得:![]() ⑩。
⑩。
(3)带电粒子在电场中的运动轨迹如图所示:
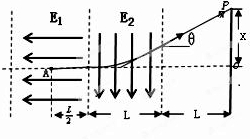
设电子打到屏上的点P到O点的距离![]() ,
,
根据上图有几何关系得: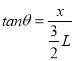 (11)
(11)
联立⑩(11)得:![]() 。
。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目