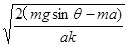题目内容
如图甲所示,斜面体固定在水平面上,倾角为θ=30°,质量为m的物块从斜面体上由静止释放,以加速度a=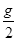 开始下滑,取出发点为参考点,则图乙中能正确描述物块的速率v、动能Ek、势能E P、机械能E、时间t、位移x关系的是( )
开始下滑,取出发点为参考点,则图乙中能正确描述物块的速率v、动能Ek、势能E P、机械能E、时间t、位移x关系的是( )

ACD
解析试题分析:物块以加速度a=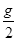 ,由静止下滑,做初速度为零的匀加速直线运动,
,由静止下滑,做初速度为零的匀加速直线运动,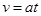 所以A正确;动能
所以A正确;动能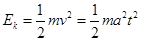 ,所以B错误;取出发点为参考点,势能
,所以B错误;取出发点为参考点,势能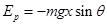 ,所以C正确;根据牛顿第二定律合力F=ma=mgsinθ,所以斜面是光滑的,满足机械能守恒,故D正确。
,所以C正确;根据牛顿第二定律合力F=ma=mgsinθ,所以斜面是光滑的,满足机械能守恒,故D正确。
考点:本题考查牛顿第二定律、匀变速运动中动能、势能、机械能的图像问题,意在考查学生的理解能力。

如图所示,螺旋形光滑轨道竖直放置,P、Q为对应的轨道最高点,一个小球以一定速度沿轨道切线方向进入轨道,且能过轨道最高点P,则下列说法中不正确的是 ( ).
| A.轨道对小球做正功,小球的线速度vP>vQ |
| B.轨道对小球不做功,小球的角速度ωP<ωQ |
| C.小球的向心加速度aP>aQ |
| D.轨道对小球的压力FP>FQ |
地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a.卫星甲、乙、丙在如图所示的三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切.不计阻力,以下说法正确的是( )
A.如果地球的转速为原来的 倍,那么赤道上的物体将会“飘”起来 倍,那么赤道上的物体将会“飘”起来 |
| B.卫星甲、乙分别经过P点时的速度相等 |
| C.卫星丙的周期最小 |
| D.卫星甲的机械能最大,卫星中航天员始终处于完全失重状态; |
一宇航员到达半径为R、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如图甲所示,现在最低点处给小球一初速度,使其绕O点在竖直平面内做圆周运动,通过传感器记录下绳中拉力大小F随时间t的变化规律如图乙所示,已知F1的大小等于7F2,引力常量为G,各种阻力不计,则( )
A.该星球表面的重力加速度为 |
B.卫星绕该星球的第一宇宙速度为 |
C.该星球的质量为 |
| D.小球通过最高点的最小速度为零 |
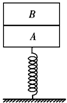
如图所示,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g,则有
| A.a1=g,a2=g |
| B.a1=0,a2=g |
C.a1=0,a2=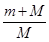 g g |
D.a1=g,a2=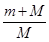 g g |
跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示.已知人的质量为50kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2.当人以360N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为
| A.a=1.0m/s2,F=260N |
| B.a=2.4m/s2,F=236N |
| C.a=3.0m/s2,F=140N |
| D.a=2.0m/s2,F=240N |