题目内容
2.一个静止的铀核${\;}_{92}^{232}$U(原子质量为232.0372u)放出一个α粒子(原子质量为4.0026u)后衰变成钍核${\;}_{90}^{228}$Th(原子质量为228.0287u).(已知:原子质量单位1u=1.67×10-27kg,1u相当于931MeV)①写出核衰变反应方程,并算出该核衰变反应中释放出的核能.
②假设反应中释放出的核能全部转化为钍核和α粒子的动能,则钍核获得的动能有多大?
分析 ①根据质量亏损,结合爱因斯坦光电效应方程求出释放的核能.
②根据动量守恒定律得出两粒子的动量大小关系,结合动能和动量的关系求出动能.
解答 解:①根据电荷数守恒、质量数守恒有:
23290U→22890 Th+24He
质量亏损△m=0.0059u
△E=△mc2=0.0059×931MeV=5.49MeV
②系统动量守恒,钍核和α粒子的动量大小相等,即根据动量守恒定律得:
pTh=pα
根据动能与动量的关系:Ek=$\frac{{P}^{2}}{2m}$EKTh+EKα
所以钍核获得的动能EKTh=$\frac{{m}_{α}}{{m}_{α}+{m}_{Th}}$
代入数据得:EKTh=0.09Mev
答:①铀核的衰变反应方程23290U→22890 Th+24He;该衰变反应中释放出的核能5.49 MeV;
②若释放的核能全部转化为新核的动能,钍核获得的动能有0.09Mev.
点评 解决本题的关键知道在核反应过程中电荷数守恒、质量数守恒,以及掌握爱因斯坦质能方程,知道在衰变的过程中动量守恒.

练习册系列答案
相关题目
13.下列说法不正确的是( )
| A. | 电场强度E=$\frac{F}{q}$和B=$\frac{F}{IL}$磁感应强度定义物理量的方法是比值定义法 | |
| B. | 互感现象是变压器工作的基础 | |
| C. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这应用了“微元法” | |
| D. | 法拉第最先引入“场”的概念,并最早发现了电流的磁效应现象 |
10.下列关于近代物理知识的描述中,正确的是( )
| A. | 处于n=3能级状态的大量氢原子自发跃迁时,能发出3种频率的光子 | |
| B. | β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| C. | 在${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{0}^{17}$O+X核反应中,X是质子,这个反应过程叫α衰变 | |
| D. | 原子核所含核子单独存在时的总质量大于该原子核的质量 |
7.物体同时受到同一平面内三个共点力的作用,下列几组力的合力可能为零的是( )
| A. | 1N、2N、4N | B. | 3N、6N、10N | C. | 4N、8N、13N | D. | 5N、12N、12N |
14.一列在y轴上振动的简谐横波沿x轴正方向传播,t=0时,平衡位置在x=0处的质元a位于平衡位置且向上振动,平衡位置在x=10.5m处的质元b位于波谷;t=1.0s时,质元a恰好第一次位于波峰,则( )
| A. | 该波的波长可能为14m | |
| B. | 该波的波速可能为10.5m/s | |
| C. | 该波由a传播到b可能历时7s | |
| D. | t=1.5s时,质元a的速度方向和加速度方向相同 |
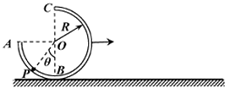 如图,半径R=1m的$\frac{3}{4}$圆形光滑管道ABC竖直放在水平地面上,C为最高点,B为最低点,管道内放一可在管道内自由移动的小球,现对管道施加一水平向右的恒力F,小球恰好可以在P点相对管道静止,此时过P点的半径OP与竖直方向的夹角为θ=30°,现再用这一装置将小球锁定在B点,管道仍在恒力F作用下从静止开始沿水平地面向右做匀加速运动,经过一段时间后管道遇一障碍突然停止运动,同时解除锁定,小球能通过管道的A点,重力加速度为g=10m/s2,小球及管道大小不计.求:
如图,半径R=1m的$\frac{3}{4}$圆形光滑管道ABC竖直放在水平地面上,C为最高点,B为最低点,管道内放一可在管道内自由移动的小球,现对管道施加一水平向右的恒力F,小球恰好可以在P点相对管道静止,此时过P点的半径OP与竖直方向的夹角为θ=30°,现再用这一装置将小球锁定在B点,管道仍在恒力F作用下从静止开始沿水平地面向右做匀加速运动,经过一段时间后管道遇一障碍突然停止运动,同时解除锁定,小球能通过管道的A点,重力加速度为g=10m/s2,小球及管道大小不计.求:
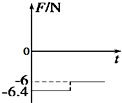
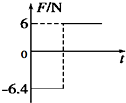
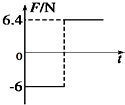
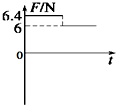
 如图所示,倾角为37°的长斜面固定在水平地面上,质量为1kg的滑块以初速度v0从斜面底端沿斜面向上滑行,取初速度方向为正方向,已知滑块与斜面间的动摩擦因数为0.8,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.则该滑块所受摩擦力Ff随时间变化的图象是( )
如图所示,倾角为37°的长斜面固定在水平地面上,质量为1kg的滑块以初速度v0从斜面底端沿斜面向上滑行,取初速度方向为正方向,已知滑块与斜面间的动摩擦因数为0.8,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.则该滑块所受摩擦力Ff随时间变化的图象是( )