题目内容
14.一列在y轴上振动的简谐横波沿x轴正方向传播,t=0时,平衡位置在x=0处的质元a位于平衡位置且向上振动,平衡位置在x=10.5m处的质元b位于波谷;t=1.0s时,质元a恰好第一次位于波峰,则( )| A. | 该波的波长可能为14m | |
| B. | 该波的波速可能为10.5m/s | |
| C. | 该波由a传播到b可能历时7s | |
| D. | t=1.5s时,质元a的速度方向和加速度方向相同 |
分析 t=0时,平衡位置在x=0处的质元位于y=0处,且向y轴向上运动,波沿x轴正方向传播,所以该点处于下坡段,平衡位置在x=10.5m处的质元b位于波谷处.可知两点平衡位置间的位移与波长的关系,注意波的周期性.
解答 解:A、t=0时,平衡位置在x=0处的质元位于y=0处,且向y轴向上运动,波沿x轴正方向传播,所以该点处于下坡段,平衡位置在x=10.5m处的质元b位于波谷处,故x=0处质元与x=10.5m处的质元平衡位置间距至少为$\frac{1}{4}$波长,所以,有:
10.5m=(n+$\frac{1}{4}$)λ
$λ=\frac{42}{4n+1}$m,(其中n=0,1,2,3…)
当n=0时,λ=42.0m;n=1时,λ=8.4m;当n=2时,λ=$\frac{14}{3}$m.故A错误;
B、x=0处的质元a位于平衡位置且向上振动,t=1.0s时,质元a恰好第一次位于波峰,可知1.0s的时间是$\frac{1}{4}$个周期,所以:T=4×1.0=4.0s.
所以该波的波速:$v=\frac{λ}{T}$=$\frac{10.5}{4n+1}$m/s,(其中n=0,1,2,3…)
当n=0时,v=10.5m/s;故B正确;
C、该波由a传播到b可能历时:$t=\frac{△x}{v}=\frac{10.5}{\frac{10.5}{4n+1}}=4n+1$s,当n=0时,t=1s;n=1时,t=5s;当n=2时,t=9s.可知,不可能是7s.故C错误;
D、由于周期T=4s,所以t=1.5s时,$\frac{1}{4}T<t<\frac{1}{2}T$,质元a正在从最大位移处向平衡位置处运动,速度的方向向下,加速度的方向也向下,所以速度方向和加速度方向相同,故D正确.
故选:BD.
点评 该题结合机械波的特点考查波速、波长与周期之间的关系,解决本题的关键是根据题目提供的条件,找出两点间的距离与波长的关系,还要注意波的周期性.

 名校课堂系列答案
名校课堂系列答案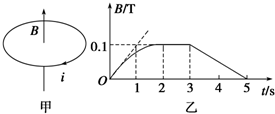 如图甲所示,在竖直向上的磁场中,水平放置一个10匝金属圆线圈,线圈所围的面积为0.15m2,线圈电阻为1Ω,磁场的磁感应强度大小B随时间t的变化规律如图乙所示,规定从上往下看顺时针方向为线圈中感应电流i的正方向.则( )
如图甲所示,在竖直向上的磁场中,水平放置一个10匝金属圆线圈,线圈所围的面积为0.15m2,线圈电阻为1Ω,磁场的磁感应强度大小B随时间t的变化规律如图乙所示,规定从上往下看顺时针方向为线圈中感应电流i的正方向.则( )| A. | 0~5s内i的最大值为0.15A | B. | 第4s末i的方向为正方向 | ||
| C. | 第3s内线圈的发热功率最大 | D. | 3~5s内线圈有扩张的趋势 |
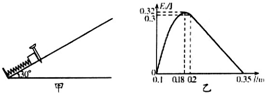 如图甲所示,一轻弹簧的下端固定在倾角为30°的足够长光滑斜面的底端,上端放一小滑块,滑块与弹簧不拴接.沿斜面向下压滑块至离斜面底端l=0.1m处后由静止释放,滑块的动能Ek,与距斜面底端的距离l的关系如图乙所示.其中从0.2m到0.35m范围内图象为直线,其余部分为曲线,不计空气阻力,取g=10m/s2.下列说法正确的是( )
如图甲所示,一轻弹簧的下端固定在倾角为30°的足够长光滑斜面的底端,上端放一小滑块,滑块与弹簧不拴接.沿斜面向下压滑块至离斜面底端l=0.1m处后由静止释放,滑块的动能Ek,与距斜面底端的距离l的关系如图乙所示.其中从0.2m到0.35m范围内图象为直线,其余部分为曲线,不计空气阻力,取g=10m/s2.下列说法正确的是( )| A. | 小滑块的质量为0.4kg | B. | 弹簧的最大形变量为0.2m | ||
| C. | 弹簧最大弹性势能为0.5J | D. | 弹簧的劲度系数为100N/m |
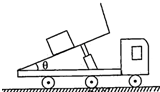 如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下,θ角逐渐增大且货物相对车厢静止,对这一过程,下列说法正确的是( )
如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下,θ角逐渐增大且货物相对车厢静止,对这一过程,下列说法正确的是( )| A. | 货物受到的摩擦力不变 | B. | 货物受到的支持力增大 | ||
| C. | 货物的机械能保持不变 | D. | 货物受到的支持力对货物做正功 |
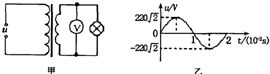 如图甲所示,一理想变压器给一个小灯泡供电.当原线圈输入如图乙所示的交变电压时,额定功率10W的小灯泡恰好正常发光,已知灯泡的电阻为40Ω,图中电压表为理想电表,下列说法正确的是( )
如图甲所示,一理想变压器给一个小灯泡供电.当原线圈输入如图乙所示的交变电压时,额定功率10W的小灯泡恰好正常发光,已知灯泡的电阻为40Ω,图中电压表为理想电表,下列说法正确的是( )| A. | 电压表的示数为220V | |
| B. | 变压器原、副线圈的匝数比为11:1 | |
| C. | 变压器的输入功率为110W | |
| D. | 副线圈两端电压的瞬时值表达式为u=20$\sqrt{2}$sinπt(V) |
 在水平地面MN上方高度为h=0.45m处有一个粗糙绝缘平台PQ,如图所示,平台上方PR右侧有水平向右的有界匀强电场,场强E=1.5×103N/C.有一质量m=1.0×10-3kg、带电量为q=-1.0×10-6C的滑块放在平台上,距离平台左端P点L=1m处,滑块与平台的滑动摩擦因数为μ=0.50.现给滑块水平向左的初速度v0=4m/s,问:
在水平地面MN上方高度为h=0.45m处有一个粗糙绝缘平台PQ,如图所示,平台上方PR右侧有水平向右的有界匀强电场,场强E=1.5×103N/C.有一质量m=1.0×10-3kg、带电量为q=-1.0×10-6C的滑块放在平台上,距离平台左端P点L=1m处,滑块与平台的滑动摩擦因数为μ=0.50.现给滑块水平向左的初速度v0=4m/s,问: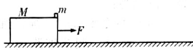 如图所示,水平地面上一质量M=10.0kg、高h=1.25m的木箱处于静止状态,在其上面最右端放一质量m=1.0kg可以视为质点的物块.已知物块与木箱、木箱与地面的滑动摩擦因数分别为μ1,μ2,且μ1=μ2=0.1,现在给木箱一个F=32N水平向右的力,使木箱和物块同时从静止开始运动,t=2s时物块脱离木箱.(取g=10m/s2)求:
如图所示,水平地面上一质量M=10.0kg、高h=1.25m的木箱处于静止状态,在其上面最右端放一质量m=1.0kg可以视为质点的物块.已知物块与木箱、木箱与地面的滑动摩擦因数分别为μ1,μ2,且μ1=μ2=0.1,现在给木箱一个F=32N水平向右的力,使木箱和物块同时从静止开始运动,t=2s时物块脱离木箱.(取g=10m/s2)求: