题目内容
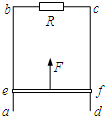 (2011?江苏模拟)如图所示,足够长的光滑导轨ab、cd固定在竖直平面内,导轨间距为l,b、c两点间接一阻值为R的电阻.ef是一水平放置的导体杆,其质量为m、有效电阻值为R,杆与ab、cd保持良好接触.整个装置放在磁感应强度大小为B的匀强磁场中,磁场方向与导轨平面垂直.现用一竖直向上的力拉导体杆,使导体杆从静止开始做加速度为
(2011?江苏模拟)如图所示,足够长的光滑导轨ab、cd固定在竖直平面内,导轨间距为l,b、c两点间接一阻值为R的电阻.ef是一水平放置的导体杆,其质量为m、有效电阻值为R,杆与ab、cd保持良好接触.整个装置放在磁感应强度大小为B的匀强磁场中,磁场方向与导轨平面垂直.现用一竖直向上的力拉导体杆,使导体杆从静止开始做加速度为| g | 2 |
(1)导体杆上升到h过程中通过杆的电量;
(2)导体杆上升到h时所受拉力F的大小;
(3)导体杆上升到h过程中拉力做的功.
分析:本题解题思路是导体杆上升到h过程中,回路面积减小,磁通量变化产生感应电动势E=
=
=
,感应电流平均值I=
,由q=I△t求电量;第二问的关键是分析导体杆受力,设ef上升到h时,速度为v1、拉力为F,感应电流瞬时值I1 根据牛顿第二定律,得F-mg-BI1l=ma;第三问由动能定理求解:WF+WG+W安=
-0
而WG=-mgh,关键是明确安培力做负功,由功能关系克服安培力做功为回路产生的电热2Q,W安=-2Q.
| △? |
| △t |
| B△s |
| △t |
| Blh |
| △t |
| E |
| 2R |
m
| ||
| 2 |
而WG=-mgh,关键是明确安培力做负功,由功能关系克服安培力做功为回路产生的电热2Q,W安=-2Q.
解答:解:(1)电量q=
△t
根据闭合电路的欧姆定律
=
根据电磁感应定律,得
=
,
导体杆上升到h过程中通过杆的电量:q=
=
(2)设ef上升到h时,速度为v1、拉力为F,根据运动学公式
=2
h,得v1=
根据牛顿第二定律,得F-mg-BI1l=ma
根据闭合电路的欧姆定律,得I1=
综上三式,得F =
+
拉力大小
+
(3)由动能定理,得WF-mgh-2Q=
-0,
导体杆上升到h过程中拉力做的功WF=
+2Q
. |
| I |
根据闭合电路的欧姆定律
. |
| I |
| ||
| 2R |
根据电磁感应定律,得
. |
| E |
| △φ |
| △t |
导体杆上升到h过程中通过杆的电量:q=
| △φ |
| 2R |
| Blh |
| 2R |
(2)设ef上升到h时,速度为v1、拉力为F,根据运动学公式
| v | 2 1 |
| g |
| 2 |
| gh |
根据牛顿第二定律,得F-mg-BI1l=ma
根据闭合电路的欧姆定律,得I1=
| Blv1 |
| 2R |
综上三式,得F =
| 3mg |
| 2 |
B2l2
| ||
| 2R |
拉力大小
| 3mg |
| 2 |
B2l2
| ||
| 2R |
(3)由动能定理,得WF-mgh-2Q=
m
| ||
| 2 |
导体杆上升到h过程中拉力做的功WF=
| 3mgh |
| 2 |
点评:电磁感应现象中的能量转化问题,分安培力做正功和做负功两种情况,本题属于安培力做负功的情况,易错的是符号.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 (2011?江苏模拟)如图所示电路,将两个相同的电流计分别改装成电流表A1(0~3A)和电流表A2(0~0.6A),把这两个电流表并连接入电路中测量电流.则下列说法中正确的是( )
(2011?江苏模拟)如图所示电路,将两个相同的电流计分别改装成电流表A1(0~3A)和电流表A2(0~0.6A),把这两个电流表并连接入电路中测量电流.则下列说法中正确的是( ) (2011?江苏模拟)利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,C、D两侧面会形成电势差UCD,下列说法中正确的是( )
(2011?江苏模拟)利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,C、D两侧面会形成电势差UCD,下列说法中正确的是( )