题目内容
（2012?怀化二模）均匀分布在地球赤道平面上空的三颗同步通信卫星能够实现除地球南北两极等少数地区外的“全球通信”．已知地球半径为R，地球表面的重力加速度为g，地球自转周期为T，同步卫星所在位置处的重力加速度为g′．下面列出的是关于卫星中任意两颗卫星间距离s的表达式，其中正确的是（ ）
分析：了解同步卫星的含义，即同步卫星的周期必须与地球相同．
通过万有引力提供向心力，列出等式通过已知量确定未知量．
根据万有引力等于重力，代换GM．
通过万有引力提供向心力，列出等式通过已知量确定未知量．
根据万有引力等于重力，代换GM．
解答：解：根据万有引力提供向心力得：
=m
r，r为轨道半径
r=
根据地球表面处万有引力等于重力得：
=mg，得：GM=gR2
根据题意画出俯视三颗同步通信卫星的几何位置图象：
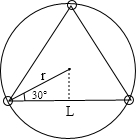
根据几何关系得：L=
r=
．
根据同步卫星处万有引力等于重力得：
=mg′，r=
由于GM=gR2
r=R
所以L=
r=
R
故选BC．
| GMm |
| r2 |
| 4π2 |
| T2 |
r=
| 3 |
| ||
根据地球表面处万有引力等于重力得：
| GMm |
| R2 |
根据题意画出俯视三颗同步通信卫星的几何位置图象：
根据几何关系得：L=
| 3 |
| 3 |
| 3 |
| ||
根据同步卫星处万有引力等于重力得：
| GMm |
| r2 |
|
由于GM=gR2
r=R
|
所以L=
| 3 |
| 3 |
|
故选BC．
点评：不同的同步卫星在地球赤道平面上空同一轨道上，画出几何图象，找出物理量的几何关系．
运用黄金代换式GM=gR2求出问题是考试中常见的方法．
运用黄金代换式GM=gR2求出问题是考试中常见的方法．
练习册系列答案
阅读快车系列答案
相关题目
（2012?怀化二模）如图所示，OA为一遵守胡克定律的弹性轻绳，其一端固定在天花板上的O点，另一端与静止在动摩擦因数恒定的水平地面上的滑块A相连．当绳处于竖直位置时，滑块A与地面有压力作用．B为一紧挨绳的光滑水平小钉，它到天花板的距离BO等于弹性绳的自然长度．现用水平力F作用于A，使之向右作直线运动，在运动过程中，作用于A的摩擦力（ ）
（2012?怀化二模）在研究性学习中，某同学设计了一个测量导电纸的导电膜厚度的实验，该同学从资料上查得导电纸导电膜材料的电阻率为ρ，并利用下列器材完成了这个实验：
（2012?怀化二模） 某列机械波在MN直线上传播，该直线上相距3m的P、Q两质点，其振动图象如图所示，则（ ）（用正确选项前的字母表示）