题目内容
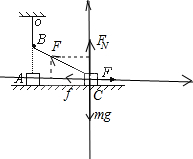
（2012?怀化二模）如图所示，OA为一遵守胡克定律的弹性轻绳，其一端固定在天花板上的O点，另一端与静止在动摩擦因数恒定的水平地面上的滑块A相连．当绳处于竖直位置时，滑块A与地面有压力作用．B为一紧挨绳的光滑水平小钉，它到天花板的距离BO等于弹性绳的自然长度．现用水平力F作用于A，使之向右作直线运动，在运动过程中，作用于A的摩擦力（ ）
分析：先对滑块在A点时受力分析，由竖直方向上合力为零可得出重力、支持力、弹性绳弹力三者关系，再对滑块在任意位置受力分析，由竖直方向受到的合力为零，得出重力、支持力、弹性绳弹力三者关系，然后结合较好知识，可得出支持力不变的结论，从而摩擦力也不变．
解答：解：
滑块在A点时，受到向下的重力mg、地面的支持力
、绳子的拉力F=k
，且有mg=k
，解得
=mg-k
当滑块运动到图示位置C时（设弹性绳与竖直方向夹角为θ），受力分析如图所示：
由滑块在竖直方向受到的合力为零可得：mg=
+k
cosθ，由图可知
cosθ=
，解
=
，即滑块受到地面的弹力不变，由f=μ
知，作用于A的摩擦力不变，所以C正确ABD错误．
故选C．
点评：解题的关键是对滑块在A点和任意位置受力分析，根据竖直方向上合力为零即可求解．
练习册系列答案
相关题目
阅读快车系列答案
（2012?怀化二模）如图所示，第一象限的某个矩形区域内，有方向垂直于纸面向里的匀强磁场B1，磁场的左边界与y轴重合，第二象限内有互相垂直正交的匀强电场与匀强磁场，其磁感应强度B2=0.5T．一质量m=l.0×10-14kg，电荷量q=1.0×10-10C的带正电的粒子以速度v=1.0×103m/s从x轴上的N点沿与x轴负方向成60°角方向射入第一象限，经P点进入第二象限内沿直线运动，一段时间后，粒子经x轴上的M点并与x轴负方向成60°角的方向飞出，M点坐标为（-0.1，0），N点坐标（0.3，0），不计粒子重力．求：
（2012?怀化二模）如图所示，相距为d的两平行金属板水平放置，开始开关S合上使平行板电容器带电．板间存在垂直纸面向里的匀强磁场．一个带电粒子恰能以水平速度v向右匀速通过两板间．在以下方法中，要使带电粒子仍能匀速通过两板，（不考虑带电粒子所受重力）正确的是（ ）
（2012?怀化二模）如图甲所示，理想变压器的原线圈电路中装有0.5A的保险丝L，原线圈匝数n1=600匝，副线圈匝数n2=120匝．当原线圈接在如图乙所示的交流电源上，要使整个电路和用电器正常工作，则副线圈两端可以接（ ）
（2012?怀化二模）如图所示，水平抛出的物体抵达斜面上端P处时，其速度方向恰好沿着斜面向下，然后沿斜面无摩擦滑下，在下图所示的图象中能正确描述物体重力的功率PG随时间t变化的图象是（ ）