题目内容
15. 足够长的粗糙绝缘板A上放一个质量为m、电荷量为+q的小滑块B.用手托住A置于方向水平向左、场强大小为E的匀强电场中,此时A、B均能静止,如图所示.现将绝缘板A从图中位置P垂直电场线移至位置Q,发现小滑块B相对A发生了运动.为研究方便可以将绝缘板A的运动简化成先匀加速接着匀减速到静止的过程.测量发现竖直方向加速的时间为1.0s,减速的时间为0.5s,P、Q位置高度差为1.5m.已知B质量m=1kg,匀强电场的场强E=0.3$\frac{mg}{q}$,A、B之间动摩擦因数μ=0.4.g取10m/s2.求:
足够长的粗糙绝缘板A上放一个质量为m、电荷量为+q的小滑块B.用手托住A置于方向水平向左、场强大小为E的匀强电场中,此时A、B均能静止,如图所示.现将绝缘板A从图中位置P垂直电场线移至位置Q,发现小滑块B相对A发生了运动.为研究方便可以将绝缘板A的运动简化成先匀加速接着匀减速到静止的过程.测量发现竖直方向加速的时间为1.0s,减速的时间为0.5s,P、Q位置高度差为1.5m.已知B质量m=1kg,匀强电场的场强E=0.3$\frac{mg}{q}$,A、B之间动摩擦因数μ=0.4.g取10m/s2.求:(1)绝缘板A加速运动和减速运动的加速度分别为多大?
(2)滑块B最后停在离出发点水平距离多大处?
(3)B滑块在A板减速过程中,B滑块机械能是变化的,变大还是变小,变化了多少?
分析 (1)根据运动学公式列方程求加速和减速的加速度大小;
(2)先以B为研究对象列牛顿第二定律方程然后以A为研究对象列牛顿第二定律方程求出加速度大小,然后根据位移公式求二者运动的距离,最后由几何关系求出滑块B最后停在离出发点水平距离.
(3)求出滑块B初末状态的动能,求出重力势能的变化,然后求出机械能的变化.
解答 解:(1)设木板A匀加速和匀减速的加速度大小分别为a1和a2,匀加速和匀减速的时间分别为t1和t2,P、Q高度差为h,
则有:a1t1=a2t2,
h=$\frac{1}{2}$a1t12+$\frac{1}{2}$a2t22,
解得:a1=2m/s2,a2=4m/s2;
(2)研究滑块B,在木板A匀减速的过程中,由牛顿第二定律可得:
竖直方向:mg-N=ma2,
水平方向:qE-μN=ma3,
解得:a3=0.6m/s2,
在这个过程中滑块B的水平位移大小为:s1=$\frac{1}{2}$a3t22=$\frac{1}{2}$×0.6×0.52=0.075m,
A减速结束时,滑块B的速度:v=a3ta2=0.6×0.5=0.3m/s,
在木板A静止后,滑块B将沿水平方向做匀减速运动,设加速度大小为a4,由牛顿第二定律得:
μmg-qE=ma4,
解得:a4=1m/s2,
该过程中滑板B的水平位移大小为:s2=$\frac{{v}^{2}}{2{a}_{4}}$=$\frac{0.{3}^{2}}{2×1}$s3=0.045m,
最后滑板B静止时离出发点的水平距离为:s=s1+s1=0.12m;
(3)A开始减速时AB的速度:vB=a1t1=2×1=2m/s,
A减速过程上升的高度:△h=$\frac{{v}_{B}}{2}$t2=$\frac{2}{2}$×0.5=0.5m,
A减速结束时B的速度:v=0.3m/s,
B机械能的变化量:△E=$\frac{1}{2}$mv2-$\frac{1}{2}$mvB2+mg△h=$\frac{1}{2}$×1×0.32-$\frac{1}{2}$×1×22+1×10×0.5=3.045J,
机械能增加了3.045J;
答:(1)木板A加速和减速的加速度分别为2m/s2和4m/s2.
(2)滑块B最后停在离出发点水平距离0.12m.
(3)B滑块在A板减速过程中,B滑块机械能变大了3.045J.
点评 本题考查了牛顿第二定律在连接体问题中的应用,关键是列牛顿第二定律方程时正确的选取研究对象受力分析,分析清楚物体的运动过程是正确解题的关键.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案 如图所示,直线A、B分别为电源a、b的路端电压与电流的关系图线,直线C为一个电阻R两端电压与电流的关系图线.将这个电阻分别接到a、b两电源上,那么( )
如图所示,直线A、B分别为电源a、b的路端电压与电流的关系图线,直线C为一个电阻R两端电压与电流的关系图线.将这个电阻分别接到a、b两电源上,那么( )| A. | 电源a的电动势较大 | |
| B. | 电源b的内阻较大 | |
| C. | R接到a电源上时电源的输出功率较大,但电源效率较低 | |
| D. | R接到a电源上时电阻的发热功率较大,电源效率也较高 |
 如图所示,现对质量为m的小球施加一拉力,让小球在B点处于静止状态,细绳与竖直方向的夹角为θ,则所需要的最小拉力F等于( )
如图所示,现对质量为m的小球施加一拉力,让小球在B点处于静止状态,细绳与竖直方向的夹角为θ,则所需要的最小拉力F等于( )| A. | mgsinθ | B. | mgcosθ | C. | mgtanθ | D. | mgcotθ |
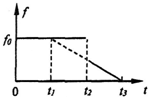
 粗糙水平面上一物体在水平拉力F作用下做匀速直线运动,从某一时刻起,拉力F随时间t变化的图象如图所示,设物体所受的最大静摩擦力f0与滑动摩擦力相等.则下列图象中可能正确描述物体所受摩擦力f随时间t变化关系的是( )
粗糙水平面上一物体在水平拉力F作用下做匀速直线运动,从某一时刻起,拉力F随时间t变化的图象如图所示,设物体所受的最大静摩擦力f0与滑动摩擦力相等.则下列图象中可能正确描述物体所受摩擦力f随时间t变化关系的是( )


 如图所示为研究平行板电容器电容决定因素的实验装置.两块相互靠近的等大正对(用S表示两极板正对面积)平行金属板M,N组成电容器,板N固定在绝缘座上并与静电计中心杆相接,板M和静电计的金属壳都接地,板M上装有绝缘手柄,可以执手柄控制板M的位置.在两板相距一定距离d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器所带电量Q不变.
如图所示为研究平行板电容器电容决定因素的实验装置.两块相互靠近的等大正对(用S表示两极板正对面积)平行金属板M,N组成电容器,板N固定在绝缘座上并与静电计中心杆相接,板M和静电计的金属壳都接地,板M上装有绝缘手柄,可以执手柄控制板M的位置.在两板相距一定距离d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器所带电量Q不变. 光滑水平面上放有如图所示的用绝缘材料制成的“┘”型滑板,(平面部分足够长),质量为4m,距滑板的A壁为L1距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦系数为μ,qE=2μmg,整个装置处于场强为E的水平匀强电场中,初始时刻,滑板与物体都静止,试求:
光滑水平面上放有如图所示的用绝缘材料制成的“┘”型滑板,(平面部分足够长),质量为4m,距滑板的A壁为L1距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦系数为μ,qE=2μmg,整个装置处于场强为E的水平匀强电场中,初始时刻,滑板与物体都静止,试求:
 如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为2m,木板质量m,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.设木板足够长,重物始终在木板上.重力加速度为g.求
如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为2m,木板质量m,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.设木板足够长,重物始终在木板上.重力加速度为g.求 水平面上固定着直角支架ABC,支架所在平面与水平面垂直,在AC和BC杆上分别套有质量为m1和m2的光滑圆环,且m1和m2用轻质细线相连,如图所示,已知AC与水平面的夹角为θ,求m1和m2平衡后,细线上的拉力.
水平面上固定着直角支架ABC,支架所在平面与水平面垂直,在AC和BC杆上分别套有质量为m1和m2的光滑圆环,且m1和m2用轻质细线相连,如图所示,已知AC与水平面的夹角为θ,求m1和m2平衡后,细线上的拉力.