题目内容
7.在“用单摆测定重力加速度”实验中,若均匀小球在垂直纸面的平面内做小幅度的摆动,若悬点到小球顶点的绳长L,小球直径为d,将激光器与传感器左右对准,分别置于摆球的平衡位置两侧,激光器连续向左发射激光束.在摆球摆动过程中,当摆球经过激光器与传感器之间时,传感器接收不到激光信号.将其输入计算机,经处理后画出相应图线.图甲为该装置示意图,图乙为所接收的光信号I随时间t变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,则该单摆的振动周期T=2t0.则当地的重力加速度大小的计算公式g=$\frac{{π}^{2}(2L+d)}{2{t}_{0}^{2}}$(用上述已知的物理量表示).若保持悬点到小球顶点的绳长L不变,改用直径为2d的另一均匀小球进行实验,则图中的t0将变大(填“变大”、“不变”或“变小”).
分析 在一个周期内两次经过平衡位置,根据该特点结合图象得出单摆的周期;根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$ 计算重力加速度.
解答 解:在一个周期内两次经过平衡位置,故周期为2t0;根据周期公式,有:
T=2π$\sqrt{\frac{L+\frac{d}{2}}{g}}$,
解得:g=$\frac{{π}^{2}(2L+d)}{2{t}_{0}^{2}}$;
改用直径2d的另一均匀小球进行实验,摆长变长,故周期变大;
故答案为:2t0,$\frac{{π}^{2}(2L+d)}{2{t}_{0}^{2}}$,变大.
点评 本题关键是看清题意,然后根据图象得到周期,再结合周期公式求解重力加速度,注意求摆长时,别忘记球的半径.

练习册系列答案
相关题目
17.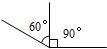 在空气和另一种折射率为n的介质的分界面上,同时发生光的反射和折射,入射光线、反射光线和折射光线的分布如图所示,则介质折射率的值可能是( )
在空气和另一种折射率为n的介质的分界面上,同时发生光的反射和折射,入射光线、反射光线和折射光线的分布如图所示,则介质折射率的值可能是( )
 在空气和另一种折射率为n的介质的分界面上,同时发生光的反射和折射,入射光线、反射光线和折射光线的分布如图所示,则介质折射率的值可能是( )
在空气和另一种折射率为n的介质的分界面上,同时发生光的反射和折射,入射光线、反射光线和折射光线的分布如图所示,则介质折射率的值可能是( )| A. | $\frac{sin45°}{sin30°}$ | B. | $\frac{sin60°}{sin30°}$ | C. | $\frac{sin60°}{sin45°}$ | D. | $\frac{sin75°}{sin45°}$ |
2.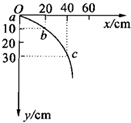 某同学在做平抛运动实验时得到了如图所示的物体运动轨迹,a、b、c三点的位置在运动轨迹上已标出,下列说法正确的是( )
某同学在做平抛运动实验时得到了如图所示的物体运动轨迹,a、b、c三点的位置在运动轨迹上已标出,下列说法正确的是( )
 某同学在做平抛运动实验时得到了如图所示的物体运动轨迹,a、b、c三点的位置在运动轨迹上已标出,下列说法正确的是( )
某同学在做平抛运动实验时得到了如图所示的物体运动轨迹,a、b、c三点的位置在运动轨迹上已标出,下列说法正确的是( )| A. | 物体做平抛运动的初速度为$\sqrt{2}$m/s | |
| B. | 物体运动到b点的速度大小为2.5m/s | |
| C. | 物体从a点运动到c点的时间为0.2s | |
| D. | 坐标原点O为平抛运动的起点 |
19.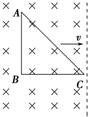 如图所示,在垂直纸面向里,磁感应强度为B的匀强磁场区域中有一个均匀导线制成的单匝直角三角形线框.现用外力使线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框的AB边始终与磁场右边界平行.已知AB=BC=l,线框导线的总电阻为R.则线框离开磁场的过程中( )
如图所示,在垂直纸面向里,磁感应强度为B的匀强磁场区域中有一个均匀导线制成的单匝直角三角形线框.现用外力使线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框的AB边始终与磁场右边界平行.已知AB=BC=l,线框导线的总电阻为R.则线框离开磁场的过程中( )
 如图所示,在垂直纸面向里,磁感应强度为B的匀强磁场区域中有一个均匀导线制成的单匝直角三角形线框.现用外力使线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框的AB边始终与磁场右边界平行.已知AB=BC=l,线框导线的总电阻为R.则线框离开磁场的过程中( )
如图所示,在垂直纸面向里,磁感应强度为B的匀强磁场区域中有一个均匀导线制成的单匝直角三角形线框.现用外力使线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框的AB边始终与磁场右边界平行.已知AB=BC=l,线框导线的总电阻为R.则线框离开磁场的过程中( )| A. | 线框中的电动势与时间成正比 | B. | 线框中的热功率与时间成正比 | ||
| C. | 通过线框截面的电荷量为$\frac{B{l}^{2}}{2R}$ | D. | 线框所受外力的最大值为$\frac{\sqrt{2}{B}^{2}{l}^{2}v}{R}$ |
16.两个大小分别为7N、4N的共点力,它们合力的大小可能是( )
| A. | 4N | B. | 12N | C. | 8N | D. | 2N |
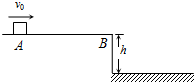 如图所示,水平台面AB距地面的高度h=1.25m.有一滑块从A点以v0=7.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.2.滑块运动到平台边缘的B点后水平飞出.已知AB长L=6.0m,不计空气阻力,g=10m/s2.求:
如图所示,水平台面AB距地面的高度h=1.25m.有一滑块从A点以v0=7.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.2.滑块运动到平台边缘的B点后水平飞出.已知AB长L=6.0m,不计空气阻力,g=10m/s2.求: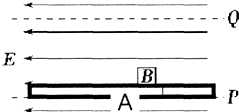 足够长的粗糙绝缘板A上放一个质量为m、电荷量为+q的小滑块B.用手托住A置于方向水平向左、场强大小为E的匀强电场中,此时A、B均能静止,如图所示.现将绝缘板A从图中位置P垂直电场线移至位置Q,发现小滑块B相对A发生了运动.为研究方便可以将绝缘板A的运动简化成先匀加速接着匀减速到静止的过程.测量发现竖直方向加速的时间为1.0s,减速的时间为0.5s,P、Q位置高度差为1.5m.已知B质量m=1kg,匀强电场的场强E=0.3$\frac{mg}{q}$,A、B之间动摩擦因数μ=0.4.g取10m/s2.求:
足够长的粗糙绝缘板A上放一个质量为m、电荷量为+q的小滑块B.用手托住A置于方向水平向左、场强大小为E的匀强电场中,此时A、B均能静止,如图所示.现将绝缘板A从图中位置P垂直电场线移至位置Q,发现小滑块B相对A发生了运动.为研究方便可以将绝缘板A的运动简化成先匀加速接着匀减速到静止的过程.测量发现竖直方向加速的时间为1.0s,减速的时间为0.5s,P、Q位置高度差为1.5m.已知B质量m=1kg,匀强电场的场强E=0.3$\frac{mg}{q}$,A、B之间动摩擦因数μ=0.4.g取10m/s2.求:
 (1)如图所示,两平行金属板A、B板间电压恒为U,一束波长为的入射光射到金属板B上,使B板发生了光电效应,已知该金属板的逸出功为W,电子的质量为m.电荷量为e,已知普朗克常量为h,真空中光速为c,下列说法中正确的是ABD
(1)如图所示,两平行金属板A、B板间电压恒为U,一束波长为的入射光射到金属板B上,使B板发生了光电效应,已知该金属板的逸出功为W,电子的质量为m.电荷量为e,已知普朗克常量为h,真空中光速为c,下列说法中正确的是ABD