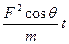题目内容
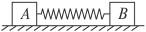
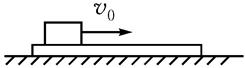
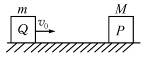
如图6所示，AB与CD为两个斜面，其上部足够长，下部分别与一个光滑的圆弧面的两端相切（OE为整个轨道的对称轴）.圆弧的圆心角为120°，半径R="2.0" m，一个物体在离弧底E高度h="3.0" m处，以速率v0="4.0" m/s沿斜面运动.若物体与斜面间的动摩擦因数μ=0.02,则该物体在AB与CD斜面上（除圆弧部分）一共能够走的路程为___________.
图6
图6
280 m (8分)
因为mgsin60°>μmgcos60°，所以物体不可能在斜面部分静止.物体沿斜面运动时，滑动摩擦力总对其做负功，使其机械能不断减少，物体沿斜面来回上升的高度越来越小，最终只能在光滑圆弧BEC部分来回运动（在B、C处时速度为0）.整个过程中滑动摩擦力大小恒定Fμ=μmgcos60°，所以摩擦力的功Wf=-Fμ·s路程，根据功能关系，其大小决定于物体机械能的变化，即Fμ·s路程=（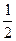
mv02+mgh)-mg·
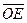(1-cos60°)
其中Fμ=μmgcos60°，重力势能参考平面为过E的水平面.
解得s路程="280" m.
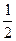mv02+mgh)-mg·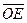(1-cos60°)其中Fμ=μmgcos60°，重力势能参考平面为过E的水平面.
解得s路程="280" m.
练习册系列答案
相关题目
