题目内容
（9分）在物理学中，常常用等效替代、类比、微小量放大等方法来研究问题。如在牛顿发现万有引力定律一百多年后，卡文迪许利用微小量放大法由实验测出了万有引力常量G的数值，图所示是卡文迪许扭秤实验示意图。卡文迪许的实验常被称为是“称量地球质量”的实验，因为由G的数值及其他已知量，就可计算出地球的质量，卡文迪许也因此被誉为第一个称量地球的人。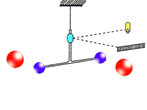
（1）若在某次实验中，卡文迪许测出质量分别为m1、m2相距为r的两个小球之间引力的大小为F，求万有引力常量G；
（2）若已知地球半径为R，地球表面重力加速度为g，万有引力常量为G，忽略地球自转的影响，请推导出地球质量及地球平均密度的表达式。
解析试题分析：（1）根据万有引力定律，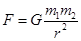
（2分）
得
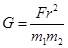（2分）
（2）设地球质量为M，在地球表面任一物体质量为m
在地球表面附近满足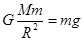
得 GM=R2g
解得地球的质量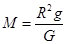
（3分）
地球的体积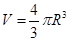
解得地球的密度 （2分）
考点：万有引力定律的应用
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
一艘宇宙飞船飞近某一新发现的行星，并进入该行星表面的圆形轨道绕行数圈后，着陆在该行星上。飞船上备有以下器材：
| A．秒表一只 | B．质量为m的物体一个 |
| C．弹簧测力计一个 | D．天平一架（带砝码） |
（1）绕行时需测量的物理量为 __，选用的器材是 _________（填序号）
（2）着陆后需测量的物理量为_______，选用的器材是 ________（填序号）
（3）利用测得的物理量写出半径R= _________，质量M=________
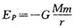，式中G为万有引力常数，M为月球的质量，m为物体的质量．求着陆器仅依靠惯性从月球表面脱离月球引力范围所需的最小速度．
