题目内容
10.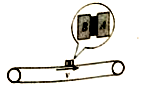 水平传送带长L=4m,以v=3m/s顺时针匀速运行.A、B两个物块(可视为质点)的质量分别为1.0kg和0.5kg,其间夹着一个只与A栓接并压紧的轻质弹簧(弹簧长度忽略不计),弹簧的弹性势能为Ep=6J,现将A、B以及弹簧整体轻放于传送带中点并瞬间弹开,两物块与传送带的动摩擦因数均为μ=0.5,g取10m/s2.求:
水平传送带长L=4m,以v=3m/s顺时针匀速运行.A、B两个物块(可视为质点)的质量分别为1.0kg和0.5kg,其间夹着一个只与A栓接并压紧的轻质弹簧(弹簧长度忽略不计),弹簧的弹性势能为Ep=6J,现将A、B以及弹簧整体轻放于传送带中点并瞬间弹开,两物块与传送带的动摩擦因数均为μ=0.5,g取10m/s2.求:(1)物块A、B弹开瞬间的速度vA和vB的大小;
(2)A、B两个物块从弹开到离开传送带所用的时间tA和tB.
分析 (1)物块A、B被弹簧弹开的过程遵守动量守恒定律和能量守恒定律,由此列式求A、B弹开瞬间的速度vA和vB的大小;
(2)物块A、B被弹簧弹开后,根据上题结果判断出A向右做匀加速运动,B向左做匀减速运动,根据速度公式求出A加速至与传送带等速时所用时间,由位移公式求出A匀加速运动的位移,共速后A做匀速运动,再由运动学公式求出匀速运动的时间,从而得到时间tA.对于物块B,先向左匀减速,再向右匀加速,最后匀速,根据牛顿第二定律和运动学公式结合求时间tB.
解答 解:(1)物块A、B被弹簧弹开的过程,取水平向右为正方向,根据动量守恒定律和能量守恒定律得:
mAvA-mBvB=0
Ep=$\frac{1}{2}$mAvA2+$\frac{1}{2}$mBvB2.
联立解得 vA=2m/s,vB=4m/s
(2)对于物块A,被弹簧弹开后做匀加速运动,由 v=vA+μgt1,有 t1=0.2s
通过的位移 x1=$\frac{v+{v}_{A}}{2}{t}_{1}$=$\frac{3+2}{2}×0.2$=0.5m<2m,所以之后A会匀速运动到传送带右端,用时 t2=$\frac{\frac{L}{2}-{x}_{1}}{v}$=$\frac{\frac{4}{2}-0.5}{3}$=0.5s
所以A物块从弹开到离开传送带所用的时间 tA=t1+t2=0.7s
对于物块B,先向左减速,用时 t3=$\frac{{v}_{B}}{μg}$=$\frac{4}{0.5×10}$=0.8s
通过的位移 x3=$\frac{{v}_{B}}{2}{t}_{3}$=$\frac{4}{2}×0.8$=1.6m
由于x3=1.6m<2m,所以之后B再向右匀加速至v.
匀加速用时 t4=$\frac{v}{μg}$=$\frac{3}{0.5×10}$=0.6s
位移 x4=$\frac{v}{2}{t}_{4}$=$\frac{3}{2}×0.6$=0.9m
之后匀速运动到传送带右端,用时 t5=$\frac{\frac{L}{2}+{x}_{3}-{x}_{4}}{v}$=$\frac{2+1.6-0.9}{3}$=0.9s
所以B物块从弹开到离开传送带所用的时间 tB=t3+t4+t5=2.3s
答:
(1)物块A、B弹开瞬间的速度vA和vB的大小分别为2m/s和4m/s;
(2)A、B两个物块从弹开到离开传送带所用的时间tA和tB分别为0.7s和2.3s.
点评 本题的关键分析清楚物体运动过程,明确各个过程的物理规律,应用动量守恒定律、牛顿第二定律和运动学公式按时间顺序进行研究.

| A. | 光电效应表明光具有能量,且具有波粒二象性 | |
| B. | 根据波尔理论可知,氢原子辐射出一个光子后,氢原子的电势能增大,核外电子的运动速度减小 | |
| C. | ${\;}_{83}^{210}Bi$的半衰期是5天,12g${\;}_{83}^{210}Bi$经过15天后衰变了1.5g | |
| D. | α粒子散射实验时卢瑟福建立原子核结构模型的重要依据 |
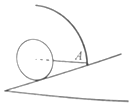 光滑斜面上固定着一根刚性圆弧形细杆,小球通过轻绳与细杆相连,此时轻绳处于水平方向,球心恰位于圆弧形细杆的圆心,如图所示,将悬点A缓慢沿杆向上移动,直到轻绳处于竖直方向,在这个过程中,轻绳的拉力( )
光滑斜面上固定着一根刚性圆弧形细杆,小球通过轻绳与细杆相连,此时轻绳处于水平方向,球心恰位于圆弧形细杆的圆心,如图所示,将悬点A缓慢沿杆向上移动,直到轻绳处于竖直方向,在这个过程中,轻绳的拉力( )| A. | 逐渐增大 | B. | 大小不变 | C. | 先增大后减小 | D. | 先减小后增大 |
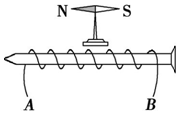 小李同学用铁钉与漆包线绕成电磁铁,当接通电路后,放在其上方的小磁针 N 极立即转向左侧,如图所示.则此时( )
小李同学用铁钉与漆包线绕成电磁铁,当接通电路后,放在其上方的小磁针 N 极立即转向左侧,如图所示.则此时( )| A. | 导线 A 端接电池负极 | |
| B. | 铁钉内磁场方向向右 | |
| C. | 铁钉左端为电磁铁的 N 极 | |
| D. | 小磁针所在位置的磁场方向水平向右 |
| A. | 单摆的周期与摆球质量、振幅无关,与摆长和当地的重力加速度有关 | |
| B. | 用光导纤维束传送信息是光的衍射的应用 | |
| C. | a、b两束光照射同一双缝干涉装置在屏上得到的干涉图样中,a光的相邻亮条纹间距小于b光的相邻亮条纹间距,则可以判断水对a光的折射率比b光大 | |
| D. | 肥皂呈现彩色条纹是光的折射现象造成的 | |
| E. | 激光测距是应用了激光平行性好的特点 |
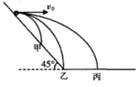 如图所示,甲、乙、丙三个小球从倾角为45°的斜面上同一点开始平抛运动,甲球落到斜面上,乙球落到斜面底端,丙球落到水平地面上,如果甲、乙、丙三个小球在水平方向上的位移之比为1:2:3,则甲、乙、丙三个小球做平抛运动的初速度之比为( )
如图所示,甲、乙、丙三个小球从倾角为45°的斜面上同一点开始平抛运动,甲球落到斜面上,乙球落到斜面底端,丙球落到水平地面上,如果甲、乙、丙三个小球在水平方向上的位移之比为1:2:3,则甲、乙、丙三个小球做平抛运动的初速度之比为( )| A. | $\sqrt{2}$:2:3 | B. | 1:2:3 | C. | $\frac{1}{2}$:2:3 | D. | $\frac{1}{\sqrt{2}}$:2:3 |
 如图所示,粗糙水平平台的台面离地高度差为h=0.8m,可看做质点的物体A、B静置在距水平平台边缘C点5m处的D点,物体A的质量m1=1kg,物体B的质量m2=2kg,物体A与水平平台间的动摩擦因数μ1=0.2,物体B与水平平台间的动摩擦因数μ2=0.1,现用水平向右的恒力F=13N推物体A,作用一段时间后撤去F,最后物体B冲出C点后的落地点与C点的水平距离为x=1.6m,重力加速度g=10m/s2,试求
如图所示,粗糙水平平台的台面离地高度差为h=0.8m,可看做质点的物体A、B静置在距水平平台边缘C点5m处的D点,物体A的质量m1=1kg,物体B的质量m2=2kg,物体A与水平平台间的动摩擦因数μ1=0.2,物体B与水平平台间的动摩擦因数μ2=0.1,现用水平向右的恒力F=13N推物体A,作用一段时间后撤去F,最后物体B冲出C点后的落地点与C点的水平距离为x=1.6m,重力加速度g=10m/s2,试求