题目内容
6.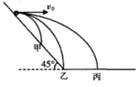 如图所示,甲、乙、丙三个小球从倾角为45°的斜面上同一点开始平抛运动,甲球落到斜面上,乙球落到斜面底端,丙球落到水平地面上,如果甲、乙、丙三个小球在水平方向上的位移之比为1:2:3,则甲、乙、丙三个小球做平抛运动的初速度之比为( )
如图所示,甲、乙、丙三个小球从倾角为45°的斜面上同一点开始平抛运动,甲球落到斜面上,乙球落到斜面底端,丙球落到水平地面上,如果甲、乙、丙三个小球在水平方向上的位移之比为1:2:3,则甲、乙、丙三个小球做平抛运动的初速度之比为( )| A. | $\sqrt{2}$:2:3 | B. | 1:2:3 | C. | $\frac{1}{2}$:2:3 | D. | $\frac{1}{\sqrt{2}}$:2:3 |
分析 三个球都做平抛运动,研究平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究,水平方向做匀速直线运动,竖直方向做自由落体运动,平抛运动落在斜面上时,竖直方向的位移和水平方向上位移比值一定,根据该规律求出平抛运动的时间求初速度之比.
解答 解:甲、乙两球都落在斜面上,竖直方向的分位移和水平方向的分位移比值一定,都有 tan45°=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$,解得:t=$\frac{2{v}_{0}}{g}$
水平位移 x=v0t=$\frac{2{v}_{0}^{2}}{g}$
甲、乙两个小球在水平方向上的位移之比为1:2,由上式可得甲、乙两个小球做平抛运动的初速度之比为1:$\sqrt{2}$=$\sqrt{2}$:2
乙、丙都落在水平面上,运动的时间相等,由x=v0t得:乙、丙两个小球做平抛运动的初速度之比为2:3.
故甲、乙、丙三个小球做平抛运动的初速度之比为$\sqrt{2}$:2:3.
故选:A
点评 解决本题的关键掌握平抛运动的规律,知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.要抓住小球落在斜面上时竖直分位移与水平分位移的比值等于斜面倾角的正切.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
11.下列说法中正确的是( )
| A. | 蹦床运动员上升到最高点时速度为零,加速度为0 | |
| B. | 宇航员随飞船绕地球做圆周运动时处于失重状态 | |
| C. | 铋210的半衰期是5天,经过15天后,20g铋还剩1.25g | |
| D. | 穿过线圈的磁通量越大,感应电动势越大 |
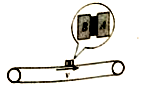 水平传送带长L=4m,以v=3m/s顺时针匀速运行.A、B两个物块(可视为质点)的质量分别为1.0kg和0.5kg,其间夹着一个只与A栓接并压紧的轻质弹簧(弹簧长度忽略不计),弹簧的弹性势能为Ep=6J,现将A、B以及弹簧整体轻放于传送带中点并瞬间弹开,两物块与传送带的动摩擦因数均为μ=0.5,g取10m/s2.求:
水平传送带长L=4m,以v=3m/s顺时针匀速运行.A、B两个物块(可视为质点)的质量分别为1.0kg和0.5kg,其间夹着一个只与A栓接并压紧的轻质弹簧(弹簧长度忽略不计),弹簧的弹性势能为Ep=6J,现将A、B以及弹簧整体轻放于传送带中点并瞬间弹开,两物块与传送带的动摩擦因数均为μ=0.5,g取10m/s2.求: 一质点做简谐运动,频率为0.5Hz,振幅为4 cm.当振子具有最大正向位移的瞬时开始计时,在图中画出振动图象.(至少一个周期)
一质点做简谐运动,频率为0.5Hz,振幅为4 cm.当振子具有最大正向位移的瞬时开始计时,在图中画出振动图象.(至少一个周期)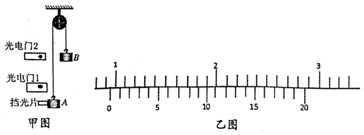
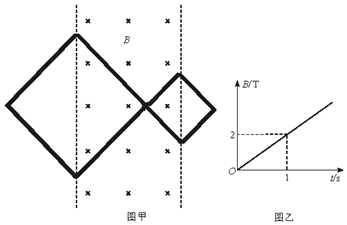 一根阻值12Ω的金属导线绕成如图甲形状的闭合回路,大正方形边长0.4m,小正方形边长0.2m,共10匝.放在粗糙的水平桌面上,两正方形对角线间存在竖直向下的匀强磁场,磁感应强度随时间变化的规律如图乙所示,整个过程中线框始终未动.求闭合回路
一根阻值12Ω的金属导线绕成如图甲形状的闭合回路,大正方形边长0.4m,小正方形边长0.2m,共10匝.放在粗糙的水平桌面上,两正方形对角线间存在竖直向下的匀强磁场,磁感应强度随时间变化的规律如图乙所示,整个过程中线框始终未动.求闭合回路 如图甲所示,可视为质点的A、B两物体置于一静止长纸带上,纸带左端与A间距为d1=0.5m,A与B间距为d2=1.5m.两物体与纸带间的动摩擦因数均为μ1=0.1,质点A、B与地面间的动摩擦因数为μ2=0.2,现以恒定的加速度a=2m/s2向右水平拉动纸带,重力加速度g=10m/s2.
如图甲所示,可视为质点的A、B两物体置于一静止长纸带上,纸带左端与A间距为d1=0.5m,A与B间距为d2=1.5m.两物体与纸带间的动摩擦因数均为μ1=0.1,质点A、B与地面间的动摩擦因数为μ2=0.2,现以恒定的加速度a=2m/s2向右水平拉动纸带,重力加速度g=10m/s2.
