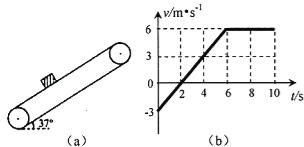��Ŀ����
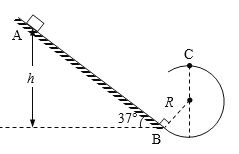
����Ŀ����ͼ��ʾ������Ϊm=0.1kg��С���ó�l=0.4m��ϸ����̶���Բ�Ĵ�����������������С��ʹ������Ĵ�С�����Բ�����������͵�A����С��6m/s�ij��ٶ�ʱ��ǡ���˶�����ߵ�B������������С�㶨����g=10m/s2����
��1��С����A��ʱ��������ʾ��
��2��С���A���˶���B������п˷������������Ĺ�
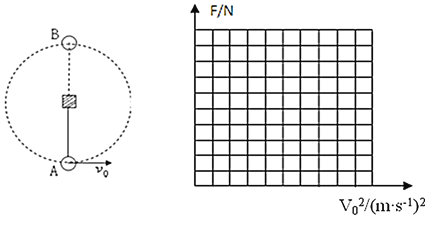
��3��С����A���Բ�ͬ�ij��ٶ�![]() ��ʼ�˶������˶���B��ʱ����������ʾ����Ӧ�Ķ���F����ͨ������������ϵ������
��ʼ�˶������˶���B��ʱ����������ʾ����Ӧ�Ķ���F����ͨ������������ϵ������![]() ͼ����
ͼ����
���𰸡���1��F=10N��2���˷�������������0.8J��
��3��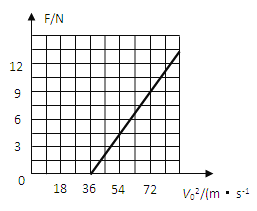
�������������������1��С����Բ���˶�����ţ�ٵڶ����ɿ��������������ʾ������2��С��ǡ�õ���B�㣬�����������������ţ�ٵڶ����ɿ������С��B����ٶȣ�Ȼ���ɶ��ܶ��������A��B�����п����������Ĺ�����3��Ӧ�ö��ܶ������С��B����ٶȣ���ţ�ٵڶ����������B������������Ȼ������ͼ����
(1) ��A�㣬��![]() �ã�
�ã� ![]()
(2) ��![]() �ã�
�ã� ![]()
С���A��B�����У����ݶ��ܶ����� ![]()
�õ�![]()
����![]()
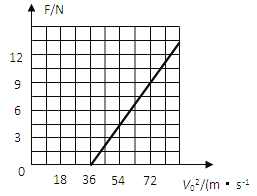
(3)С���A��B�����У����ݶ��ܶ����� ![]()
С������ߵ�![]()
��ʽ�����ã� ![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��

��ϰ��ϵ�д�
�����Ŀ