题目内容
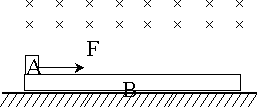
如图所示，在光滑的水平面上静止着一个绝缘的、足够长的木板B，质量为mB＝2 kg，木板上有一质量为mA＝1 kg，带电量为q＝＋0.2C的滑块A，空间有磁感应强度大小为B＝5T、方向垂直纸面向里的范围足够大的匀强磁场．A与B之间的动摩擦因数μ＝0.8，现在对滑块A加一水平向右的恒力F＝9 N，重力加速度g＝10 m/s2．求：
(1)从恒力F作用开始，经过t＝
s时，B受到的摩擦力大小？
(2)当A的速度达到vA＝8 m/s时，A、B加速度各为多大？
答案：
解析：
解析：
|
设A、B的速度为v0时，AB间即将要滑动 取A、B整体为对象，根据牛顿第二定律： 取B为对象，根据牛顿第二定律： 代数据得： 加速到v0所需时间 ①当t＝ 取B为对象，根据牛顿第二定律： ②因VA＞V0，故AB间出现滑动． N＝mg－qB晇A f2＝μN代数据，得f2＝1.6N 对A利用牛顿第二定律：F－f2＝mAaAaA＝7.4m/s2 对B利用牛顿第二定律：f2＝mBaBaA＝0.8m/s2 |
s时，A、B间末滑动，故取AB为对象
练习册系列答案
相关题目
如图所示，在光滑的水平板的中央有一光滑的小孔，用不可伸长的轻绳穿过小孔，绳的两端分别挂上小球C和物体B，在B的下端再挂一重物A，现使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时圆周运动的半径为R，现剪断连接A、B的绳子，稳定后，小球以另一半径在水平面上做匀速圆周运动，则下列说法正确的是（ ）
如图所示，在光滑的水平板的中央有一光滑的小孔，一根不可伸长的轻绳穿过小孔．绳的两端分别拴有一小球C和一质量为m的物体B，在物体B的下端还悬挂有一质量为3m的物体A．使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时，圆周运动的半径为R．现剪断连接A、B的绳子，稳定后，小球以2R的半径在水平面上做匀速圆周运动，则下列说法正确的（ ）
如图所示，在光滑的水平板的中央有一光滑的小孔，用不可伸长的轻绳穿过小孔，绳的两端分别栓上一小球C和一物体B，在B的下端再悬挂一重物A，现使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时，圆周运动半径为R．现剪断连接AB的绳子，稳定后，小球以另一半径在水平面上做匀速圆周运动，则下列说法正确的是（ ）
