题目内容
14.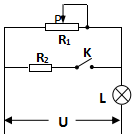 如图所示的电路中,R2=6Ω,灯L的电阻为4Ω,其额定功率为16W,电源电压U=12V,闭合电键K后,调节变阻器滑动头P至R1中点处,灯L恰能正常发光.求:
如图所示的电路中,R2=6Ω,灯L的电阻为4Ω,其额定功率为16W,电源电压U=12V,闭合电键K后,调节变阻器滑动头P至R1中点处,灯L恰能正常发光.求:(1)滑动变阻器R1的最大阻值?
(2)此时若断开电键K,灯的电功率?
(3)断开K后,要使灯仍正常发光,变阻器的阻值应为多大?
分析 (1)根据功率公式求出灯L的额定电流,由欧姆定律求出R1的最大阻值.
(2)根据串联电路分压规律求出灯L的电压,再求其功率.
(3)灯要正常发光,其电压必须等于额定电压,求出灯L的额定电压,得到变阻器的电压,从而求得变阻器的阻值.
解答 解:(1)对灯L,由PL=IL2RL,得灯L的额定电流为:
IL=$\sqrt{\frac{{P}_{L}}{{R}_{L}}}$=$\sqrt{\frac{16}{4}}$=2A
额定电压为:UL=ILRL=2×4V=8V
并联电路的电压为:U1=U-UL=12-8=4V
由欧姆定律得:$\frac{\frac{1}{2}{R}_{1}{R}_{2}}{\frac{1}{2}{R}_{1}+{R}_{2}}$=$\frac{{U}_{1}}{{I}_{L}}$
解得R1的最大阻值为:R1=6Ω
(2)若断开电键K,灯的电压为:UL′=$\frac{{R}_{L}}{{R}_{L}+\frac{1}{2}{R}_{1}}$U=$\frac{4}{4+3}$×12V=$\frac{48}{7}$V
灯的电功率为:P=$\frac{{U}_{L}^{′2}}{{R}_{L}}$=$\frac{(\frac{48}{7})^{2}}{4}$≈11.75W
(3)断开K后,要使灯仍正常发光,变阻器的阻值设为R.
此时电路中电流等于IL,变阻器的电压为:UR=U-UL=12-8=4V
所以有:R=$\frac{{U}_{R}}{{I}_{L}}$=$\frac{4}{2}$Ω=2Ω
答:(1)滑动变阻器R1的最大阻值是6Ω.
(2)此时若断开电键K,灯的电功率是11.75W.
(3)断开K后,要使灯仍正常发光,变阻器的阻值应为2Ω.
点评 对于直流电路的计算问题,要搞清电路的结构,明确各个元件之间的关系,熟练运用串联与并联的特点求电流或电压是关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | 4m/s2 | B. | 5m/s2 | C. | 20m/s2 | D. | 100m/s2 |
| A. | $-\frac{{7{E_1}}}{144}$ | B. | $\frac{{7{E_1}}}{144}$ | C. | $-\frac{15}{16}{E_1}$ | D. | $\frac{15}{16}{E_1}$ |
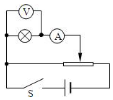 描绘小灯泡伏安特性曲线的实验原理如图所示,下列关于该实验的说法中正确的是( )
描绘小灯泡伏安特性曲线的实验原理如图所示,下列关于该实验的说法中正确的是( )| A. | 系统误差是由于电压表 V 的分流引起的 | |
| B. | 由实验数据画出的伏安特性曲线是一条过原点的倾斜直线 | |
| C. | 实验得到的伏安特性曲线,说明导体的电阻随温度的升高而增大 | |
| D. | 因为小灯泡电阻太小,为安全起见,要选阻值尽量大的滑动变阻器 |
| A. | 当某点与点电荷距离r→0时,该点场强E→∞ | |
| B. | 当某点与点电荷间距离r→∞时,该点电场强度E→∞ | |
| C. | 没有两个点的场强是相同的 | |
| D. | 与点电荷距离相等的点处的场强是相同的 |
| A. | 由 E=$\frac{F}{q}$可知,某电场的场强 E 与 q 成反比,与 F 成正比 | |
| B. | 正负试探电荷在同一点受到的电场力方向相反,所以某一点场强方向与试探电荷的正负有关 | |
| C. | 电场中某一点的场强与放入该点的试探电荷正负无关 | |
| D. | 电场中某一点不放试探电荷时,该点场强等于零 |
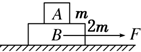 如图所示,水平面上放置质量分别为m、2m的A、B两个物体,A、B间,B与地面间动摩擦因数均为μ,最大静摩擦力等于滑动摩擦力,现用水平拉力F拉B,使A、B一起以同一加速度运动,则拉力F的最大值为( )
如图所示,水平面上放置质量分别为m、2m的A、B两个物体,A、B间,B与地面间动摩擦因数均为μ,最大静摩擦力等于滑动摩擦力,现用水平拉力F拉B,使A、B一起以同一加速度运动,则拉力F的最大值为( )| A. | 6μmg | B. | 3μmg | C. | μmg | D. | 4μmg |
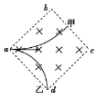 如图,两个带电量、质量均相同的带电粒子甲、乙以不同的速率从a点沿对角线ac方向射入正方形匀强磁场中,磁场方向垂直纸面向里,甲粒子垂直bc离开磁场,乙粒子从d点离开磁场,不计粒子重力,则( )
如图,两个带电量、质量均相同的带电粒子甲、乙以不同的速率从a点沿对角线ac方向射入正方形匀强磁场中,磁场方向垂直纸面向里,甲粒子垂直bc离开磁场,乙粒子从d点离开磁场,不计粒子重力,则( )| A. | 甲粒子带正电,乙粒子带负电 | |
| B. | 甲粒子的速率是乙粒子速率的$\sqrt{2}$倍 | |
| C. | 甲粒子所受的洛伦兹力是乙粒子所受洛伦兹力的2倍 | |
| D. | 甲粒子在磁场中的运行时间是乙粒子在磁场中运动时间的一半 |