题目内容
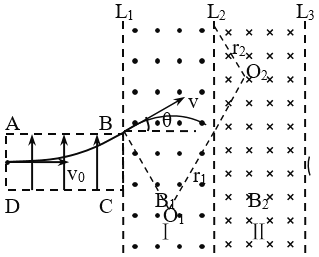
【题目】如图所示,在矩形区域ABCD内存在竖直向上的匀强电场,在BC右侧Ⅰ、Ⅱ两区域存在匀强磁场,L1、L2、L3是磁场的边界(BC与L1重合),宽度相同,方向如图所示,区域Ⅰ的磁感强度大小为B1。一电荷量为q、质量为m(重力不计)的带正电点电荷从AD边中点以初速度v0沿水平向右方向进入电场,点电荷恰好从B点进入磁场,经区域Ⅰ后又恰好从与B点同一水平高度处进入区域Ⅱ。已知AB长度是BC 长度的![]() 倍。
倍。
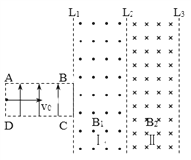
(1)求带电粒子到达B点时的速度大小;
(2)求磁场的宽度L;
(3)要使点电荷在整个磁场中运动的时间最长,求区域Ⅱ的磁感应强度B2。
【答案】(1)![]() ;(2)
;(2)![]() ;(2)B2≥1.5B1。
;(2)B2≥1.5B1。
【解析】(1)设点电荷进入磁场时的速度大小为v,与水平方向成θ角,由类平抛运动的速度方向与位移方向的关系有:
tanθ=![]()
则θ=30°
根据速度关系有:v=![]()
(2)设点电荷在区域Ⅰ中的轨道半径为r1,由牛顿第二定律得:
![]()
轨迹如图:
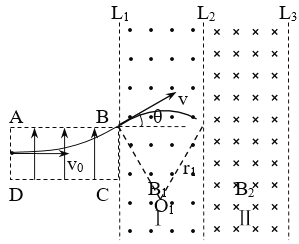
由几何关系得:L=r1
解得:L=![]()
(3)当点电荷不从区域Ⅱ右边界离开磁场时,点电荷在磁场中运动的时间最长。设区域Ⅱ中最小磁感应强度为B,对应的轨迹半径为r2,轨迹如图:
同理得: ![]()
根据几何关系有:L=r2(1+sinθ)
解得:B=1.5B1

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目