题目内容
如图所示，一连接体一端与一小球相连，绕过O点的水平轴在竖直平面内做圆周运动，设轨道半径为r，图中P、Q两点分别表示小球轨道的最高点和最低点，则以下说法正确的是（ ）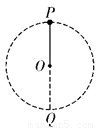
A．若连接体是轻质细绳时，小球到达P点的速度可以为零
B．若连接体是轻质细杆时，小球到达P点的速度可以为零
C．若连接体是轻质细绳时，小球在P点受到细绳的拉力不可能为零
D．若连接体是轻质细杆时，小球在P点受到细杆的作用力为拉力，在Q点受到细杆作用力为推力
【答案】分析：细绳只能表现为拉力，细杆可以表现为拉力，也可以表现为支持力，在最高点和最低点，靠竖直方向上的合力提供向心力，根据速度的大小判断连接体表现为什么力．
解答：解：A、若连接体是细绳，在P点的临界情况是拉力为零，根据mg=m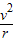
，最小速度为
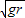．故A错误；
B、若连接体是细杆，可以提供向上的支持力，若重力等于支持力时，在P点的最小速度为零．故B正确；
C、当小球在P点的速度为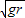
时，绳子的拉力为零，故C错误；
D、若连接体是细杆，小球在P点可以表现为拉力，也可以表现为支持力，在Q点只能表现为拉力．故D错误．
故选B．
点评：解决本题的关键掌握竖直平面内圆周运动的临界情况，掌握向心力的来源，运用牛顿第二定律进行求解．
解答：解：A、若连接体是细绳，在P点的临界情况是拉力为零，根据mg=m
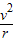，最小速度为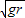．故A错误；B、若连接体是细杆，可以提供向上的支持力，若重力等于支持力时，在P点的最小速度为零．故B正确；
C、当小球在P点的速度为
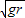时，绳子的拉力为零，故C错误；D、若连接体是细杆，小球在P点可以表现为拉力，也可以表现为支持力，在Q点只能表现为拉力．故D错误．
故选B．
点评：解决本题的关键掌握竖直平面内圆周运动的临界情况，掌握向心力的来源，运用牛顿第二定律进行求解．
练习册系列答案
相关题目
（2007?汕头模拟）如图所示，横截面为四分之一圆（半径为R）的柱体放在水平地面上，一根匀质木棒OA长为3R，重为G．木棒的O端与地面上的铰链连接，木棒搁在柱体上，各处摩擦均不计．现用一水平推力F作用在柱体竖直面上，使柱体沿着水平地面向左缓慢移动．问：
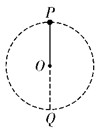如图所示，一连接体一端与一小球相连，绕过O点的水平轴在竖直平面内做圆周运动，设轨道半径为r，图中P、Q两点分别表示小球轨道的最高点和最低点，则以下说法正确的是（ ）
如图所示，水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m．在轨道所在空间存在水平向右的匀强电场，电场线与轨道所在的平面平行，电场强度E=1.0×104N/C．现有一电荷量q=+1.0×10-4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点ΧPB=2.5m处由静止释放，带电体恰好能通过半圆形轨道的最高点C，然后落至水平轨道上的D点．取g=10m/s2．