题目内容

【题目】如图所示，一个固定在竖直平面上的光滑半圆形管道，管道里有一个直径略小 于管道内径的小球，小球在管道内做圆周运动，从 B 点脱离后做平抛运动，经过 t=1s 后 又恰好与倾角为 450的斜面垂直相碰．已知圆轨道半径为 R=5m，小球的质量为 m=5kg．求

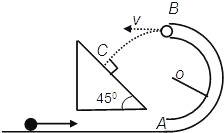
（1）小球在斜面上的相碰点 C 与 B 点的水平距离；

（2）小球经过圆弧轨道的 B 点时，对轨道作用力的大小和方向。

【答案】（1）10m（2）50N

【解析】

（1）根据平抛运动时间求得在C点竖直分速度，然后由速度方向求得v，即可根据平抛运动水平方向为匀速运动求得水平距离；
（2）对小球在B点应用牛顿第二定律求得支持力NB的大小和方向。

（1）根据平抛运动的规律，小球在C点竖直方向的分速度
vy=gt=10m/s

水平分速度vx=vytan450=10m/s
则B点与C点的水平距离为：x=vxt=10m

（2）根据牛顿运动定律，在B点

NB+mg=m

解得 NB=50N

根据牛顿第三定律得小球对轨道的作用力大小N, =NB=50N

方向竖直向上

练习册系列答案
相关题目

【题目】如图，直角坐标xOy平面内，有一半径为R的圆形匀强磁场区域，磁感应强度的大小为B，方向垂直于纸面向里，边界与x、y轴分别相切于a、b两点。一质量为m，电荷量为q的带电粒子从b点沿平行于x轴正方向进入磁场区域，离开磁场后做直线运动，经过x轴时速度方向与x轴正方向的夹角为60°，下列判断正确的是( )

A. 粒子带正电 B. 粒子在磁场中运动的轨道半径为R

C. 粒子运动的速率为 D. 粒子在磁场中运动的时间为

【题目】长为L的平行金属板水平放置,两极板带等量的异种电荷,板间形成匀强电场,一个带电量为+q、质量为m的带电粒子,以初速度v0紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时速度恰与下极板成30°角,如图所示,不计粒子重力.

(1).粒子末速度的大小;

(2).匀强电场的场强;

(3).两板间的距离.

【题目】将一厚度不计粗细均匀的导热性能良好的长直玻璃管水平固定在桌面上，现用一厚度不计的活塞封闭一定质量的理想气体，已知活塞与玻璃管之间的摩擦可忽略不计。已知外界大气压强为p，封闭气柱的长度为L，外界环境温度为T。现用质量不计的细绳跨过光滑的定滑轮连接活塞与质量为m的重物，连接活塞的细绳呈水平状态，当系统再次平衡时，活塞向右移动的距离为。假设整个过程中外界大气压强恒为p，重力加速度大小为g。求：

①玻璃管的横截面积为多大？

②当外界环境的温度降为时，系统再次达到平衡，气柱的长度为多少？

【题目】做磁共振(MRI)检查时，对人体施加的磁场发生变化时会在肌肉组织中产生感应电流。某同学为了估算该感应电流对肌肉组织的影响，将包裹在骨骼上的一圈肌肉组织等效成单匝线圈，线圈的半径r＝5.0 cm，线圈导线的截面积A＝0.80 cm2，电阻率ρ＝1.5 Ω·m。如图所示，匀强磁场方向与线圈平面垂直，若磁感应强度B在0.3 s内从1.5 T均匀地减为零，求(计算结果保留一位有效数字)

(1)该圈肌肉组织的电阻R；

(2)该圈肌肉组织中的感应电动势E；

(3)0.3 s内该圈肌肉组织中产生的热量Q。

【题目】如图所示，质量为m，边长为L的正方形线框，在有界匀强磁场上方h高处由静止自由下落，线框的总电阻为R，磁感应强度为B的匀强磁场宽度为2L．线框下落过程中，ab边始终与磁场边界平行且处于水平方向．已知ab边刚穿出磁场时线框恰好做匀速运动．求：

（1）cd边刚进入磁场时线框的速度;

（2）线框穿过磁场的过程中，产生的焦耳热．

【题目】质点沿x轴运动，其速度v随时间t变化的v-t图像如图所示，已知t=0时刻质点速度方向沿x轴正方向；t2－t1= t3－t2。则下列说法正确的是

A. t2时刻质点的速度和加速度均为零

B. t2时刻质点即将向x轴负方向运动

C. 质点在t1时刻和t3时刻的速度相同

D. 质点在t1时刻和t3时刻的加速度大小相等方向相反

【题目】关于理想气体，液体和热力学定律，下列说法正确的是_____________。

A．理想气体除了碰撞外，分子间没有作用力

B．那些不容易液化的气体在常温常压下可以看成理想气体

C．液体沸腾时候的温度被称为沸点，沸腾属于汽化现象

D．理想气体对外做功同时吸热，理想气体内能一定减小

E．不可能从单一热源取热使之完全转换为有用的功

【题目】a、b、c、d是匀强电场中的四个点，它们正好是一个矩形的四个顶点.电场线与矩形所在平面平行。已知a点的电势为20 V，b点的电势为24 V，d点的电势为4 V，如图由此可知c点的电势为 V

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网