题目内容
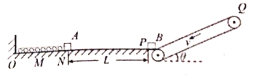
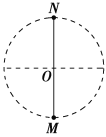
【题目】一长度为2R的轻质细杆两端分别连接质量为m和2m、可视为质点的球M、N，细杆的中点O处有一轴，细杆可绕其在竖直面内无摩擦地转动，开始细杆呈竖直状态，N处在最高点，如图所示，当装置受到很小的扰动后，细杆开始绕过中点的轴转动，则在球N转动到最低点的过程中，下列说法中正确的是(重力加速度取g=10m/s2)( )
A.N的机械能减少量等于M的机械能增加量
B.N的重力势能减少量等于M的重力势能增加量
C.运动过程中两球的最大速度均为
D.细杆对N做的功为
【答案】ACD
【解析】
A．两球组成的系统只有重力做功，系统机械能守恒，重力势能和动能相互转化，所以N的机械能减少量等于M的机械能增加量，故A正确；
B．两球运动过程中竖直位移大小相等，质量不同，重力做功不同，重力势能变化量的大小不同，故B错误；
C．球N转动到最低点，速度最大，根据机械能守恒定律：
解得：
，故C正确；
D．对N小球应用动能定理：
解得细杆对N做的功为：
，故D正确。
故选ACD．
练习册系列答案
相关题目
