题目内容
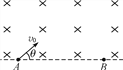
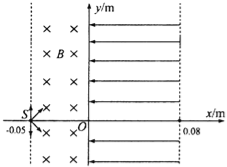
【题目】如图所示,在xOy直角坐标平面内﹣0.05m≤x<0的区域有垂直纸面向里的匀强磁场,磁感应强度B=0.4T,0≤x≤0.08m的区域有沿﹣x方向的匀强电场.在x轴上坐标为(﹣0.05m,0)的S点有一粒子源,它一次能沿纸面同时向磁场内每个方向发射一个比荷![]() =5×107C/kg,速率v0=2×106m/s的带正电粒子.若粒子源只发射一次,其中只有一个粒子Z恰能到达电场的右边界,不计粒子的重力和粒子间的相互作用(结果可保留根号).求:
=5×107C/kg,速率v0=2×106m/s的带正电粒子.若粒子源只发射一次,其中只有一个粒子Z恰能到达电场的右边界,不计粒子的重力和粒子间的相互作用(结果可保留根号).求:
(1)粒子在磁场中运动的半径R;
(2)粒子Z从S发射时的速度方向与磁场左边界的夹角θ;
(3)第一次经过y轴的所有粒子中,位置最高的粒子P的坐标;
(4)若粒子P到达y轴瞬间电场突然反向,求粒子P到达电场右边界时的速度.
【答案】(1)粒子在磁场中运动的半径R为0.1m;
(2)粒子Z从S发射时的速度方向与磁场左边界的夹角θ为60°或120°;
(3)第一次经过y轴的所有粒子中,位置最高的粒子P的坐标为(0,![]() m);
m);
(4)若粒子P到达y轴瞬间电场突然反向,粒子P到达电场右边界时的速度为大小2![]() m/s,方向与电场右边界成45°或135°.
m/s,方向与电场右边界成45°或135°.
【解析】试题分析:(1)粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则有
![]()
可得![]()
(2)由题意可知Z粒子是垂直电场左边界进入电场的,作出Z粒子在磁场中的运动轨迹如图1所示,O1为轨迹圆的圆心.分别用dB表示磁场区域的宽度.由几何知识可知,∠O1SO=θ,在△SOO1中满足: ![]() ,得 θ=60°
,得 θ=60°
即粒子Z从S发射时的速度方向与磁场左边界的夹角θ为60°或120°.
(3)在y轴上位置最高的粒子P的运动轨迹恰与y轴相切于N点,如图2所示,N点到x轴的竖直距离L满足: L2+(R-dB)2=R2;
解得: ![]() 即粒子P的位置坐标为(0,
即粒子P的位置坐标为(0, ![]() ).
).
(4)用dE表示电场的宽度.对Z粒子在电场中运动,由动能定理有: ![]() ①
①
代入数据解得:E=5.0×105N/C
设沿电场方向的速度为v⊥,则![]() ;
;
qE=ma
解得 v⊥=2×106m/s
所以粒子P到达电场右边界时的速度![]()
方向与电场右边界成45°或135°

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案【题目】某试验小组为了探究通电长直导线产生的磁场的磁感应强度B与导线上电流强度I0和距离r间的关系,设计了如下的试验:一根固定通电长直导线通以可调节的电流强度I0,一根可以自由运动的短导线与之在同一平面内,通以恒定的电流I=2A,长度L=0.1m,应用控制变量法:
(1)使两导线距离r保持不变,调节长直导线中的电流强度I0,测得相应的磁场力F,得到如下实验数据:
试验次数 | 1 | 2 | 3 | 4 | 5 |
电流强度I0/A | 5.0 | 10 | 15 | 20 | 25 |
磁场力F/×10-4N | 1.01 | 2.00 | 2.98 | 3.96 | 5.02 |
磁感应强度B/×10-3T | _______ | _______ | _______ | _______ | _______ |
填充上述表格中的磁感应强度B一栏的值,并归纳磁感应强度B和产生磁场的长直导线上的电流I0的关系是______________.
(2)使长直导线中的电流强度I0保持不变,调节短导线与之的距离r,测得相应的磁场力F,得到如下实验数据:
试验次数 | 1 | 2 | 3 | 4 | 5 |
距离r/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 |
磁场力F/×10-4N | 12.0 | 5.9 | 4.1 | 3.0 | 2.4 |
磁感应强度B/×10-3T | _______ | _______ | _______ | _______ | _______ |
填充上述表格中的磁感应强度B一栏的值,并归纳磁感应强度B和空间位置与长直导线间的距离r的关系是______________.