题目内容
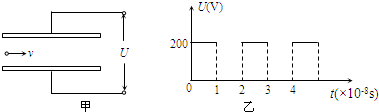
4. 如图所示,一个初动能为Ek的带电粒子a(不计重力),水平射入两块带等量异种电荷的平行金属板间,飞出时动能为3Ek.如果该粒子飞出时的动能变为4.5Ek,则该粒子射入时的速度大小应变为原来的( )
如图所示,一个初动能为Ek的带电粒子a(不计重力),水平射入两块带等量异种电荷的平行金属板间,飞出时动能为3Ek.如果该粒子飞出时的动能变为4.5Ek,则该粒子射入时的速度大小应变为原来的( )| A. | 1.5倍 | B. | 2倍 | C. | 3倍 | D. | 4倍 |
分析 两个过程中带电粒子做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,两过程初速度不同故在磁场中运动时间不同,在竖直方向的位移不同,最后用动能定理求解.
解答 解:设粒子第一个过程中初速度为v0,极板的长度为L,则有:Ek=$\frac{1}{2}m{v}_{0}^{2}$.
第一个过程中沿电场线方向的位移为:y1=$\frac{1}{2}$a($\frac{L}{{v}_{0}}$)2;
第一个过程由动能定理得:qEy1=3Ek-Ek
第二个过程的末动能为4.5Ek,设其初速度为nv0.
第二个过程中沿电场线方向的位移为:y2=$\frac{1}{2}$a($\frac{L}{n{v}_{0}}$)2=$\frac{1}{{n}^{2}}{y}_{1}$
由动能定理得:-qEy2=4.5Ek-$\frac{1}{2}m(n{v}_{0})^{2}$=4.5Ek-n2•Ek
解得:n=2
即该粒子射入时的速度大小应变为原来的2倍.
故选:B.
点评 本题是动能定理和类平抛运动知识的综合应用,用相同的物理量表示电场力做功是解题的关键.

练习册系列答案
相关题目
9.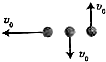 如图所示,三个完全相同的小球在同一高度处以相同大小的初速度v0分别水平、竖直向下、竖直向上抛出.不计空气阻力,下列说法正确的是( )
如图所示,三个完全相同的小球在同一高度处以相同大小的初速度v0分别水平、竖直向下、竖直向上抛出.不计空气阻力,下列说法正确的是( )
 如图所示,三个完全相同的小球在同一高度处以相同大小的初速度v0分别水平、竖直向下、竖直向上抛出.不计空气阻力,下列说法正确的是( )
如图所示,三个完全相同的小球在同一高度处以相同大小的初速度v0分别水平、竖直向下、竖直向上抛出.不计空气阻力,下列说法正确的是( )| A. | 小球飞行过程中单位时间内的速度变化量相同 | |
| B. | 从开始运动至落地,重力对小球做功相同 | |
| C. | 小球落地时,重力的瞬时功率均相同 | |
| D. | 从开始运动至落地,重力对小球做功的平均功率相同 |
3.以下说法中正确的是( )
| A. | 增透膜是利用了光的色散现象 | |
| B. | 白光通过三棱镜后形成彩色光带是利用了光的干涉现象 | |
| C. | 电子表的液晶显示是利用了光的偏振现象 | |
| D. | 用标准平面检查光学仪器表面的平整程度是利用了光的衍射现象 |
20.下列说法正确的是( )
| A. | 物体温度升高时,物体中分子的平均动能可能不变 | |
| B. | 可以从单一热库吸收热量,使之完全变为功,而不产生其他影响 | |
| C. | 第二类永动机不可制成,是因为违反了能量守恒定律 | |
| D. | 夏天,将密封有空气的矿泉水瓶放进低温的冰箱中会变扁,此过程中瓶内空气内能减少,外界对其做正功 |
1.下列物理量中,属于标量的是( )
| A. | 向心加速度 | B. | 电势 | C. | 电场强度 | D. | 线速度 |
 如图所示,在xoy平面第一象限的整个区域分布碰上匀强磁场,电场方向平行于y轴向下,在第四象限内存在有界(含边界)匀强磁场,其左边界为y轴,右边界为x=$\frac{5}{2}$l的直线,磁场方向垂直纸面向外,一质量为m、电荷量为q、可看作质点的带正电粒子,从y轴上P点以初速度v0垂直于y轴射入匀强电场,在电场力作用下从x轴上Q点以与x轴正方向成45°角进入匀强磁场,已知OQ=l,不计粒子重力,求:
如图所示,在xoy平面第一象限的整个区域分布碰上匀强磁场,电场方向平行于y轴向下,在第四象限内存在有界(含边界)匀强磁场,其左边界为y轴,右边界为x=$\frac{5}{2}$l的直线,磁场方向垂直纸面向外,一质量为m、电荷量为q、可看作质点的带正电粒子,从y轴上P点以初速度v0垂直于y轴射入匀强电场,在电场力作用下从x轴上Q点以与x轴正方向成45°角进入匀强磁场,已知OQ=l,不计粒子重力,求: